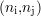3.6 Le rapport signal sur bruit

La mesure de la dynamique des signaux CF peut servir à quantifier la « qualité » de ces signaux, lorsqu’il s’agit d’une comparaison à une référence commune réalisée dans des conditions similaires, comme à la section précédente. Si au contraire les conditions de mesure varient, les signaux correspondants n’ont pas de lien entre eux et comparer la dynamique n’a plus aucun sens physique. C’est pourquoi une autre mesure est souvent utilisée : le rapport signal sur bruit (RSB).

3.6.1 Pourquoi quantifier la qualité d’un signal ?

Les acquisitions faites dans le cadre de ces travaux balayent des conditions de mesure assez larges. En particulier, trois conditions de mesure seront considérées dans la suite :

• deux technologies de microbobines sont utilisées (cf. section 2.2) ;
• cinq stratégies d’émission-réception sont mises en œuvre (cf. section 2.5) ;
• une dizaine de fréquences d’excitation sont appliquées (cf. sous-section 2.3.1).

Il est utile d’essayer de déterminer l’influence de chacune de ces trois conditions de mesure, en termes d’efficacité de la sonde à multiéléments, notamment afin de pouvoir déterminer le jeu de conditions le plus efficace s’il existe.

Ces classements doivent être effectués selon un ou des critères objectifs, calculables pour toutes les conditions de mesure, à partir de chaque signal CF ou de l’ensemble des acquisitions. Le chapitre 4 met en place un algorithme de détection et une méthode permettant de quantifier la qualité statistique de détection d’un grand nombre de signaux CF acquis dans des conditions identiques. Un calcul plus simple et individuel peut consister à l’établissement du rapport signal sur bruit de chaque signal CF.

3.6.2 Le calcul du rapport signal sur bruit

Le bruit de la mesure dépend très fortement des trois conditions de mesure. En effet, le bruit de mesure est supérieur en général dans cette application au bruit de quantification de l’impédancemètre (quantum numérique d’échantillonnage de 1 mΩ). Il est donc lié principalement à la transimpédance de la sonde « à vide », qui est fonction de ces conditions de mesure. La qualité du signal CF considéré est directement affectée par le niveau de bruit, et il est nécessaire de le prendre en compte pour quantifier cette qualité.

La qualité d’un signal dépend aussi directement de la dynamique du signal. Si, pour une dynamique donnée, la qualité du signal est inversement proportionnelle au niveau de bruit, à l’opposé, pour un niveau de bruit donné, la qualité du signal est proportionnelle à sa dynamique. Une définition appelée PSNR (peak signal-to-noise ratio, rapport signal maximal sur bruit) reprend cette idée et s’exprime pour un signal s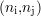 à valeur moyenne nulle¹² par

où zhd est la zone hors défaut, choisie distinctement de la zone de signal utile et suffisamment éloignée du défaut pour que l’hypothèse que le défaut n’influence pas le signal puisse être vérifiée et ℓ_zhd est la taille totale en points de mesure de cette zone. L’utilisation du logarithme permet de réduire l’échelle de valeurs, ce qui est particulièrement utile quand les dynamiques à comparer sont différentes de plusieurs ordres de grandeur. Le PSNR est exprimé en décibels.

Cependant, le calcul du PSNR accorde une grande influence à un unique point de mesure parmi l’ensemble, celui pour lequel la valeur du signal est la plus grande. Si une erreur de mesure arrive sur ce point précis, elle est directement reportée dans l’expression et la valeur finale du PSNR. Le calcul est par conséquent peu robuste vis-à-vis du bruit. Pour remédier à ce problème, le calcul du RSB choisi prend en compte les valeurs du signal CF sur une « zone de défaut » zd, centrée sur la position du défaut et d’une taille toujours identique¹³, correspondant à la zone de signal utile. La valeur efficace du signal CF est calculée sur cette zone, ce qui donne

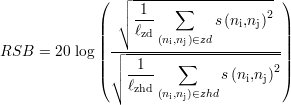
où ℓ_zd est la taille totale en points de mesure de cette zone.

Pour analyser ces valeurs de RSB, un critère reconnu est le critère de Rose[BSLB01] : si la valeur de RSB est inférieure à 7 dB¹⁴, alors il sera difficile de reconnaître l’information cherchée au sein du signal, à cause d’un bruit trop important. Ce critère est expérimentalement assez bien vérifié sur les acquisitions réalisées.

3.6.3 Comparaison des conditions de mesure

Le calcul du RSB permet de comparer la qualité des signaux CF et par suite l’efficacité de la sonde en fonction des conditions de mesure. La figure 3.18 présente les résultats obtenus pour l’ensemble des stratégies d’émission-réception, en fonction de la fréquence des courants d’excitation et pour chacune des deux technologies de microbobines. Chaque défaut correspond à un signal de dynamique différente, de RSB différent : un seul défaut est pris en compte pour les valeurs portées par ces courbes. Il s’agit du défaut « exemple », d’une longueur de 200 μm sui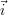vant l’axe , d’une profondeur de 400 μm et d’une largeur de 100 μm suivant l’axe 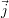. Néanmoins, tous les résultats des comparaisons obtenus dans cette sous-section ont été vérifiés comme valables pour l’ensemble des acquisitions.

Deux stratégies d’émission-réception se détachent assez nettement des autres : les stratégies différentielles, ERE- et RER offrent globalement de plus importants RSB. Ensuite, les stratégies absolues à plusieurs éléments, ERE+ et ER sont équivalentes, en particulier pour la sonde à bobines micromoulées. Cela est certainement dû à la précision de la mesure, qui a été a priori meilleure pour cette technologie de microbobines, des effets de types résonance ayant quelque peu perturbé certaines acquisitions faites avec les microbobines CI¹⁵. Enfin, ces courbes montrent que la stratégie à microbobine seule est beaucoup moins efficace que les autres, à tel point que le critère de Rose s’applique pour la plupart des fréquences avec la sonde à microbobines CI.

Pour chacun des deux types de sonde, la forte correspondance des deux meilleures courbes s’explique par le fait que les deux stratégies sont en réalité équivalentes en considérant chaque groupe de deux microbobines émission-réception séparément. Comme cela a été vu à la sous-section 3.1.1.2, les deux groupes dans le cas de la stratégie ERE- fonctionnent indépendamment, réalisant au sein de l’image CF chacun des deux lobes. Il en est de même dans le cas de la stratégie RER, ce qui conduit à un fonctionnement global identique.

En termes de fréquence, les conclusions sont différentes en fonction de la technologie des microbobines utilisée :

• Pour la sonde à microbobines CI, 3 MHz est la meilleure fréquence.
• Pour la sonde à bobines micromoulées, une plage de fréquences allant globalement de 4 MHz à 7 MHz semble donner des résultats équivalents.

Cette différence s’explique par les géométries et les propriétés électriques des éléments sensibles.

Enfin, il est utile de signaler que dans le cas du défaut « exemple », le RSB maximal obtenu est 22,5 dB. En fonction de la dimension des défauts, la valeur du RSB varie, comme indiqué dans le tableau 3.1. La sonde à bobines micromoulées reste plus efficace que la sonde à microbobines CI pour l’ensemble des dimensions. Ceci n’était pas prévisible par l’étude simple des caractéristiques théoriques déterminées précédemment dans le tableau 2.1. En effet, les produits des pouvoirs d’émission et des sensibilités sont équivalents pour les deux technologies de microbobines. Cependant, la sensibilité des microbobines CI est calculée en négligeant l’espacement entre les 8 couches : la dernière couche par exemple se situe à plus d’un millimètre de la surface à inspecter. La sensibilité réelle des microbobines CI est certainement bien moindre. Ceci conduit à des plus grands RSB pour les mesures effectuées par la sonde à bobines micromoulées.

Tous ces résultats correspondent à des acquisitions réalisées sans aucune amplification, avec des courants d’intensité efficace 10 mA pour les microbobines CI et 5 mA pour les bobines micromoulées. En particulier, tout défaut débouchant de dimension supérieure à 100 μm est contrôlé par les bobines micromoulées sans amplification avec un RSB supérieur à 8 dB.

3.6.4 Influence de l’orientation

Le RSB d’un signal CF dépend des dimensions du défaut correspondant, mais aussi de son orientation. Pour les conditions de mesures optimales obtenues précédemment, à savoir l’utilisation de la sonde à bobines micromoulées dans la stratégie ERE-, des courbes de RSB sont tracées à la figure 3.19 en fonction de la fréquence pour le plus gros défaut et le défaut « exemple ». Le tableau 3.2 liste les valeurs optimales des RSB correspondant à ces courbes.

Les courbes ont toutes la même forme, avec un maximum assez plat entre environ 4 et 7 MHz. Le défaut parallèle à l’axe principal de la sonde (mode m_∥i) est celui donnant la plus importante valeur de RSB, tandis que celui perpendiculaire au même axe (mode m_⊥i) produit très souvent le plus faible RSB, d’autant plus lorsque le défaut est de grandes dimensions. La combinaison des deux modes de mesure (mode m_c,i) permet d’obtenir un très bon compromis. Les défauts o_i-j et o_i+j (modes m_∥ij et m_⊥ij) sont logiquement équivalents en termes de RSB. Leur combinaison (mode m_c,ij) donne un RSB comparable.

3.6.5 Influence de la décimation

Un signal CF décimé possède a priori moins d’informations que le signal CF original. La section 3.5 explique que le suréchantillonnage arrive à reconstruire le signal original si le facteur de décimation est inférieur ou égal à 3, et que le résultat est optimal pour un facteur de suréchantillonnage n_e = n_d.

Par analogie avec les dynamiques relatives moyennes et minimales définies par les équations 3.8 et 3.9, il est possible de définir un RSB relatif moyen¹⁶ par

où RSB_nd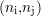 est le RSB du signal CF décimé d’un facteur n_d et auquel appartient le point de mesure aux coordonnées originales (n_i,n_j) et comme à la sous-section 3.4.3, RSB₁ = RSB₁(1,1). En valeur minimale, cela devient

La figure 3.20 montre le calcul de ces deux grandeurs pour le défaut « exemple ». Le RSB semble en moyenne beaucoup moins sensible à la décimation que la dynamique. Cependant, à partir de n_d = 5, au moins un des signaux décimés produit un RSB diminué de près de 2 dB, diminution qui vaut plus de 5 dB dès n_d = 7. À l’inverse, comme précédemment le théorème de Nyquist-Shannon (cf. sous-section 3.4.2) est bien respecté, car la diminution maximale de RSB vaut à peine 0,1 dB pour n_d ≤ 3, ce qui est négligeable.