2.2 Les deux technologies de microbobines

Cette expérimentation a été effectuée avec des microbobines carrées de deux technologies différentes :

• des microbobines sur circuit imprimé multicouches et de largeur égale à 2,6 mm, comportant des pistes larges sur un faible nombre de spires par couche ;
• des bobines micromoulées de largeur égale à 1 mm, aux pistes beaucoup plus fines sur un grand nombre de spires pour une couche unique.

Ces deux technologies ont été choisies pour leur complémentarité et leur représentativité des alternatives actuelles : si la première est intéressante car largement éprouvée et de faible coût, la deuxième représente une technologie en cours de développement, à la fois plus chère et aux perspectives de performances renouvelées.

2.2.1 Les microbobines sur circuit imprimé

Les premières microbobines utilisées sont de type circuit imprimé (CI) huit couches, fabriquées industriellement par la société Linea Connect. Elles représentent les meilleures caractéristiques couramment obtenues pour cette technologie standard. Le matériel utilisé est une ligne de huit microbobines indépendantes, visibles sur la figure 2.2.

2.2.1.1 Caractérisation géométrique

Chaque microbobine est constituée en fait de huit bobines plates superposées, reliées en série, réparties sur une épaisseur totale de 1,25 mm. Chaque couche a un côté de longueur c = 2,6 mm, des pistes de largeur ℓ_p = 100 μm et d’épaisseur e_p = 25 μm, et comporte n = 5 spires distribuées sur toute sa surface avec un espacement de e = 100 μm. La figure 2.3 montre une vue schématique d’une microbobine obtenu par le logiciel de conception Orcad ainsi qu’une une vue de coupe. Les connexions sont effectuées par deux plots ronds de 1 mm de diamètre.

Il est intéressant pour la suite de la caractérisation de calculer aussi les deux grandeurs géométriques que sont la longueur développée de piste et la surface totale effective. La longueur développée ou longueur totale de piste peut être calculée par la formule

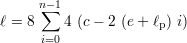(2.1)

(dans laquelle le 8 correspond aux 8 couches). La surface totale effective, qui est la surface équivalente de l’ensemble des spires, s’écrit

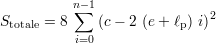(2.2)

Pour cette géométrie, ℓ vaut 288 mm et S_totale vaut 142 mm².

2.2.1.2 Caractérisation électrique

Cette géométrie confère à ces bobines une impédance fortement inductive. Le diagramme de Bode de l’impédance mesurée d’une microbobine CI avec la connectique de l’expérimentation (décrite ci-après à la sous-section 2.3.1) est présenté à la figure 2.4. Il montre en effet un déphasage compris entre 70 et 90˚ entre 500 kHz et 12 MHz. Cette figure présente aussi l’évolution mesurée de la résistance R en fonction de la fréquence f, ainsi que la partie imaginaire X et l’inductance L telle que

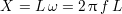
Modèle théorique Un modèle macroscopique théorique largement admis d’une microbobine est présenté à la figure 2.5. L est l’inductance de la bobine, R la résistance des pistes et C représente l’ensemble des capacités parasites, comprenant en particulier les capacités inter-spires. La résistance vaut expérimentalement environ 5 Ω et l’inductance L est comprise expérimentalement entre 2,5 μH et 1,5 μH. Une approximation¹ de la valeur de C peut être calculée grâce à l’expression de la capacité entre deux conducteurs de surface S, séparés par la distance e :

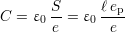(2.3)

Ici, il vient

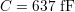
Le modèle est un dipôle RLC dont l’impédance s’écrit

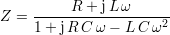
ou, sous forme normalisée,

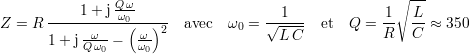
En supposant le facteur de qualité Q grand, le calcul de la fréquence de résonance f_r la donne proche de la fréquence propre f₀ du dipôle. Il vient

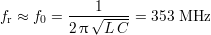(2.4)

Cette valeur, très supérieure aux fréquences utilisées pour ces travaux, justifie que le phénomène de résonance ne soit pas visible dans les graphes de la figure 2.4.

Le calcul de C et f_r est effectué pour la bobine seule, c’est-à-dire sans prendre en compte la connectique associée qui est utilisée pour l’obtention du diagramme de Bode de l’impédance. L’influence de cette connectique est forte, comme le prouve la diminution des valeurs de l’inductance et de la résistance mesurées lorsque la fréquence est supérieure à 8 MHz. Ce phénomène, qui n’est pas dû à la capacité parasite des microbobines mais à l’ensemble des connexions et des câbles, entraîne une limitation dans la plage des fréquences utilisables.

2.2.1.3 Caractérisation de l’élément sensible

En tant qu’élément de sonde, les caractéristiques géométriques et électriques ne suffisent pas à qualifier complètement le comportement physique. Un élément peut être soit récepteur soit émetteur. Dans le premier cas, il est utile de déterminer sa sensibilité et son bruit. Dans le second cas, le calcul du pouvoir d’émission est nécessaire.

La sensibilité d’un capteur est le rapport des variations respectives de la grandeur de sortie du capteur et du mesurande. Dans le cas d’une bobine utilisée comme capteur magnétique, un champ magnétique est transformé en tension. La sensibilité s’écrit, d’après la loi 1.7 de Lenz-Faraday, à la fréquence f

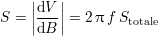(2.5)

où S_totale est la surface totale de l’ensemble des spires de la bobine. Pour les microbobines CI, la sensibilité à f = 1 MHz vaut

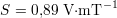
Le bruit d’une bobine lorsqu’elle n’est pas parcourue par un courant est uniquement un bruit d’agitation thermique. Cette tension efficace s’écrit, à la température T et sur une plage de fréquences de mesure Δf

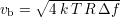(2.6)

où k = 1,38 ⋅ 10^-23 J⋅K^-1 est la constante de Boltzmann. La bande passante Δf à prendre en compte est celle sur laquelle est faite la mesure : il s’agit en général de l’intersection de la bande passante de l’éventuel dernier filtre de l’instrumentation et de celle de l’appareil de mesure. Sans a priori sur l’instrumentation, il est raisonnable de poser au maximum Δf = 10 MHz², ce qui donne à T = 298 K

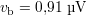
Il est possible de rapporter cette grandeur au mesurande. Il suffit pour cela de la diviser par la sensibilité, obtenant alors la valeur efficace de bruit magnétique équivalent, qui vaut ici

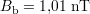
Le pouvoir d’émission, dans le cas d’un élément émetteur, est le rapport entre le champ émis et le courant nécessaire à son émission. Son expression s’obtient à l’aide de celle du flux magnétique Φ produit par un élément d’inductance L traversé par un courant I, qui s’écrit avec B supposé uniforme sur l’ensemble de la surface effective de la bobine

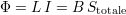
ce qui donne

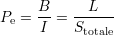(2.7)

Ainsi apparaît la notion de densité surfacique d’inductance. Cela signifie que plus l’inductance d’une bobine est « concentrée », plus son pouvoir d’émission est grand. Ici, avec les valeurs données précédemment,

2.2.2 Les microbobines micromoulées

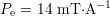
La seconde technologie de microbobines est issue des techniques de réalisation de microsystèmes, plus complexes que les techniques de CI. Il s’agit de microbobines réalisées par micromoulage de cuivre sur un substrat de silicium. Ces microbobines ont été développées par l’Institut d’Électronique Fondamentale (IEF, Orsay), laboratoire de l’Université Paris-Sud, avec lequel depuis plusieurs années une collaboration est en cours[RWJ⁺07].

Le substrat sur lequel sont gravées les microbobines peut être de deux types, en silicium (support rigide, 280 μm d’épaisseur) ou en kapton (support souple, 50 μm d’épaisseur). Seul le premier type de substrat est utilisé dans ces travaux, mais il est utile de noter que le second donnera la possibilité dans un futur proche d’améliorer les performances des microbobines pour le CND : le décollement sera plus faible et ce substrat souple permettra de se conformer à des géométries de pièces non planes[CD07].

2.2.2.1 Procédé de fabrication

Le procédé de fabrication de ces microbobines se découpe en 6 grandes étapes[Woy05, WGDG⁺06]. La figure 2.6 montre schématiquement ces étapes.

1. La première étape est une étape de métallisation. Après nettoyage de la surface du substrat à l’aide de solvants, une sous-couche métallique de cuivre, d’une épaisseur de 100 nm, est déposée par évaporation sous vide. Cela consiste à bombarder un fil de cuivre avec un faisceau d’électrons énergétiques, ce qui entraîne l’arrachage des atomes de cuivre. Ils viennent alors se déposer sur le substrat situé en face du dispositif. Cette sous-couche sert uniquement à rendre possible le dépôt électrolytique de l’étape 5.
2. La deuxième étape est une enduction de résine, à l’aide d’une tournette atmosphérique. Cet enrésinement est suivi d’un recuit thermique. L’épaisseur de résine après enduction et recuit est de 18,5 μm. Cette étape et les deux suivantes font partie de la technique de lithographie UV.
3. La troisième étape, l’insolation, consiste à éclairer l’échantillon pendant une durée déterminée, avec une lumière monochromatique. L’insolation est réalisée à travers un masque sur lequel sont inscrites les pistes en négatif. Ainsi seule la résine située à l’endroit des pistes subit l’attaque de la lumière.
4. Pour terminer la lithographie UV, un développement est opéré, pendant lequel la résine insolée est dissoute par un bain dans un liquide développeur. Les échantillons sont ensuite rincés et séchés sous flux d’azote.
5. Le dépôt électrolytique de cuivre est l’étape la plus importante et la plus critique. L’opération est effectuée en mode galvanostatique : un courant d’intensité constante traverse une solution électrolytique très acide, de pH inférieur à 1, par l’intermédiaire d’une anode et d’une cathode respectivement constituées d’une plaque de cuivre et de l’échantillon. Une réaction d’oxydation a lieu à l’anode, libérant un ion Cu²⁺ qui réagira ensuite dans une réduction au niveau de la cathode, selon les réactions suivantes :

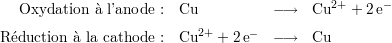
   ce qui entraîne le dépôt d’un atome de cuivre sur la pièce. La réduction ne pouvant avoir lieu que sur une surface conductrice (dont des électrons sont arrachés), seule la partie de la pièce non protégée par la résine réagit : les pistes se dessinent ainsi lors de cette réaction. Toute la difficulté de cette étape réside dans la nécessaire constance de dépôt en termes de section tout au long de la piste.

6. Enfin, la gravure de la sous-couche métallique est la dernière étape du procédé. Assez délicate elle aussi, elle est essentielle puisqu’elle sert à isoler les spires des microbobines. Après avoir dissout le moule en résine par immersion dans l’acétone, puis rincé l’échantillon à l’éthanol, il faut supprimer les zones de la sous-couche anciennement protégées. Pour ce faire, l’échantillon est plongé dans un bain acide commercial qui grave le cuivre restant de façon uniforme en commençant par les bords : au bout de quelques minutes la sous-couche de 100 nm d’épaisseur a disparu sans que les pistes ne soient encore trop déformées.

2.2.2.2 Caractérisation géométrique

Les bobines micromoulées sont des microbobines carrées, dont la largeur c d’un côté vaut 1 mm et qui comportent n = 40 spires. La largeur et l’espacement des pistes valent cette fois ℓ_p = e = 5 μm, tandis que l’épaisseur des pistes de cuivre a été fixée à e_p = 20 μm. La figure 2.7 montre une photographie traditionnelle (appareil photo numérique monté sur une loupe binoculaire) d’une des barrettes de quatre microbobines utilisées. La figure 2.8 montre une photographie provenant d’un microscope électronique à balayage d’une de ces microbobines. Les plots de connexion sont des carrés de 100 μm de côté.

Les formules 2.1 et 2.2 appliquées ici donnent ℓ = 98 mm et S_totale = 17 mm².

2.2.2.3 Caractérisation électrique

Contrairement à la technologie CI, le micromoulage permet d’obtenir des pistes très fines. Cela a pour effet d’augmenter l’inductance grâce à l’augmentation possible du nombre de spires, les deux étant fortement liés[Bry55, Ter43]. Afin d’obtenir la plus grande inductance possible, le nombre de spires est maximisé par le remplissage complet de la surface disponible.

Ceci a pour conséquence d’augmenter fortement la résistance. En effet, pour un conducteur ohmique classique, la résistance s’écrit

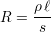
où ρ est la résistivité du conducteur, ℓ sa longueur développée et s sa section. Pour un encombrement donné, plus la bobine comportera de spires, plus la longueur développée de conducteur sera importante et, surtout, plus la section sera faible : ces deux paramètres tendent à augmenter la résistance. Le défaut de ces bobines est donc d’avoir une forte résistance, ce qui est relativement perturbateur pour nos mesures : augmentation du bruit thermique à la réception, augmentation des dissipations thermiques par effet Joule à l’émission...

Le diagramme de Bode de l’impédance présenté à la figure 2.9 confirme le fait qu’à une fréquence inférieure à 5,5 MHz, la partie résistive (réelle) de l’impédance est plus grande que la partie inductive (imaginaire), et la phase est inférieure à 45˚.

Les graphes représentant la résistance R et l’inductance L ont globalement la même allure que pour les microbobines CI, comme l’indique la figure 2.4). R est ici beaucoup plus élevée et vaut environ 55 Ω, tandis que la valeur de l’inductance L est assez proche à 1,7 μH. Ceci est possible grâce au grand nombre de spires, augmentant la surface effective totale. Les équations 2.3 et 2.4 ont ici pour résultat

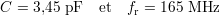
La valeur de C est cependant largement sous-estimée, car la capacité interspires considérée pour les microbobines CI (cf. sous-section 2.2.1.2) est maintenant en parallèle d’une capacité bobine - substrat. Cette capacité est de l’ordre de quelques centaines de pF[Woy05] et s’ajoute à C. Il vient alors que la fréquence de résonance f_r est plus proche de quelques dizaines de MHz.

Le phénomène capacitif dû à l’instrumentation et à la connectique associées est observé de la même façon qu’il l’avait été dans le cas des microbobines CI.

2.2.2.4 Caractérisation de l’élément sensible

De même que pour les microbobines CI, il est possible d’utiliser les définitions 2.5 à 2.7 pour déterminer les caractéristiques de l’élément de mesure. Il vient dans les mêmes conditions

2.2.2.5 Intégration

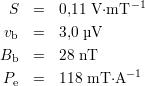
La soudure à l’étain étant impossible sur les plots de 100 μm de côté, le substrat de silicium a été collé, après un clivage au plus près des bobines, sur un support constitué d’un circuit imprimé intermédiaire où ont été gravées des pistes en cuivre d’une largeur de 0,8 mm de large pour 5 mm de long. Les connexions ont alors été réalisées par microsoudage par ultrasons d’un fil d’aluminium de 25 μm de diamètre.

2.2.3 Comparaison des deux technologies

Les valeurs des caractéristiques géométriques, électroniques et de l’élément sensible sont résumées pour les deux technologies utilisées dans le tableau 2.1. La miniaturisation des microbobines micromoulées est défavorable sur deux points : la sensibilité est 8 fois plus faible et le bruit est 28 fois plus grand. Cependant, ces inconvénients sont limités par le fait que le niveau de bruit est très faible dans les deux cas, inférieur au bruit apporté en général par l’instrumentation, donc peu perturbateur. De plus, le calcul de bruit thermique est réalisé sur une plage étendue de fréquences et par conséquent très fortement surestimé : en pratique pour cette étude, une détection synchrone décrite à la sous-section 2.3.1 réduit la plage Δf à quelques dizaines de hertz.

En outre, la résolution est a priori nettement améliorée par les bobines micromoulées : en effet, elle est grossièrement proportionnelle à la surface d’encombrement, qui est 8 fois plus faible pour cette technologie. Le pouvoir d’émission est lui inversement proportionnel à la surface effective totale, ce qui signifie qu’une bobine CI émettra un champ plus faible à courant égal. Cependant, grâce à une épaisseur de piste plus grande, un courant plus important peut physiquement circuler dans les microbobines CI. En pratique, à des niveaux de tension et des fréquences comparables, le courant est environ deux fois plus important dans les microbobines CI.