
[Suivant] [Précédent] [Fin] [Niveau supérieur]
Le fonctionnement d’une sonde pour le CND par courants de Foucault (CF) est régi par des phénomènes physiques complexes et non linéaires, qu’il convient d’expliciter avant d’exposer en détail les avantages et inconvénients de cette technique.
Une sonde CF peut être divisée en deux parties. L’émetteur est en général constitué d’une bobine parcourue par un courant d’excitation Iexc, qui produit un champ électromagnétique déterminé par les équations de Maxwell :

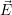 et
et 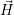 sont respectivement les champs électrique et magnétique,
sont respectivement les champs électrique et magnétique, 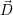 et
et 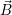 les inductions électrique et
magnétique,
les inductions électrique et
magnétique, 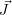 la densité surfacique de courant électrique et ρ la densité volumique de charges
électriques.
la densité surfacique de courant électrique et ρ la densité volumique de charges
électriques.
Ici, les courants de déplacement représentés par la quantité 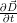 dans l’équation de Maxwell-Ampère sont
négligeables. En effet, l’Approximation des Régimes Quasi-Statiques (ARQS) énonce qu’il est possible de
négliger le temps de propagation des ondes électromagnétiques si les dimensions considérées sont faibles
devant la longueur d’onde. Les fréquences utilisées généralement pour le CND par courants de Foucault et
plus particulièrement dans ces travaux ne sont pas supérieures à 20 MHz, ce qui correspond à une longueur
d’onde
dans l’équation de Maxwell-Ampère sont
négligeables. En effet, l’Approximation des Régimes Quasi-Statiques (ARQS) énonce qu’il est possible de
négliger le temps de propagation des ondes électromagnétiques si les dimensions considérées sont faibles
devant la longueur d’onde. Les fréquences utilisées généralement pour le CND par courants de Foucault et
plus particulièrement dans ces travaux ne sont pas supérieures à 20 MHz, ce qui correspond à une longueur
d’onde
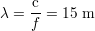
car la vitesse de propagation des ondes dans le matériau est assimilable à celle c = 3 ⋅ 105 km ⋅ s-1 de la lumière dans le vide. Cette longueur d’onde peut être considérée très grande devant les longueurs de propagation des ondes, inférieures au centimètre.
Les matériaux considérés dans cette étude étant des milieux linéaires isotropes, les relations constitutives
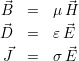
En prenant en compte l’absence de charges électriques dans ce cas de figure et en supposant les milieux non diélectriques (ε constante, égale à la permittivité du vide ε0) et non saturés (μ indépendante de la valeur de H), les quatre équations de Maxwell deviennent
Ces équations entraînent la création, par le champ magnétique ayant pénétré à l’intérieur de la pièce, de courants induits au sein de cette pièce. En régime harmonique, ces courants sont à la même fréquence que le champ et donc à la même fréquence que le courant inducteur. Ces courants sont représentés sur la figure 1.7 dans l’exemple d’une bobine excitatrice.
Dans le cas canonique d’une pièce conductrice à surface plane, où l’induction est réalisée par un champ d’excitation uniformément orienté de type onde plane transverse électromagnétique, la résolution de ces équations est possible analytiquement[PCS89]. Elle indique que les lignes de courants sont situées dans des plans parallèles à la surface de la pièce. La densité de ces courants varie en fonction de la profondeur z à laquelle ils se trouvent. Si la pièce est semi-infinie ou suffisamment épaisse, cette densité est donnée par
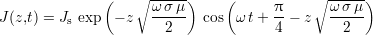 | (1.5) |
où Js est l’amplitude de la densité des courants induits au niveau de la surface de la pièce et ω la pulsation associée au courant excitateur, comme montré par la figure 1.8. Cette équation montre que l’amplitude de la densité des courants induits varie de façon exponentielle en fonction de la profondeur, avec une grandeur caractéristique
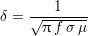 | (1.6) |
correspondant à la distance au-delà de laquelle les courants induits ont perdu 63% de leur amplitude. Cette longueur est appelée « profondeur de pénétration » ou « épaisseur de peau », et est essentielle dans la compréhension du fonctionnement du CND par CF.
|
|
Pour la plupart des autres configurations, calculer la densité J(z,t) des courants de Foucault demande des développements analytiques[DD68] ou numériques conséquents, comme par exemple le calcul par éléments finis[CSLBM07a] ou par intégrales de volume[BSS89]. Dans le cas de courants créés par un solénoïde, les courants induits sont des boucles qui peuvent être au mieux situées dans des plans parallèles à la surface de la pièce (cf. figure 1.7). Ils ne peuvent pas exactement être explicités par l’équation 1.5. Cependant, la décroissance de l’amplitude des courants induits existe toujours et l’épaisseur de peau, en tant que grandeur caractéristique, est habituellement encore exprimée par l’équation 1.6[Mot90].
De plus, l’équation 1.5 décrit le déphasage entre le courant d’excitation et le courant induit à la profondeur z comme une fonction affine de cette profondeur. Ceci reste aussi globalement vrai avec un inducteur solénoïde.
Les courants ainsi créés suivent des chemins à l’image de spires virtuelles situées à l’intérieur du matériau conducteur. Ils engendrent donc à leur tour un champ électromagnétique de réaction, qui s’oppose au champ d’excitation. Ce champ est présent au niveau de la sonde. Son amplitude dépend en particulier de la circulation des courants de Foucault dans la pièce.
Dans le cas d’une sonde à fonction double, l’impédance de la bobine est perturbée dès lors que celle-ci est traversée par ce champ électromagnétique de réaction[BJSS91]. Il existe alors une valeur d’impédance « hors défaut », autour de laquelle sont mesurées les variations par un impédancemètre branché aux bornes de la bobine. Il mesure la tension à ses bornes et la divise par le courant d’excitation qui la traverse.
Dans le cas d’une sonde à fonctions séparées où l’élément récepteur est une bobine, le champ électromagnétique total crée une différence de potentiel entre les bornes de cette bobine. Il s’agit d’une force électromotrice générée par la loi de Lenz-Faraday, qui peut s’écrire
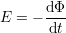 | (1.7) |
pour une spire, où Φ est le flux de l’induction magnétique 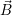 à travers la surface de la spire. Il est alors
possible de mesurer la transimpédance de la sonde qui est le rapport de la tension de réception
sur le courant d’excitation. Ainsi, les deux méthodes sont équivalentes en termes de grandeur
mesurée.
à travers la surface de la spire. Il est alors
possible de mesurer la transimpédance de la sonde qui est le rapport de la tension de réception
sur le courant d’excitation. Ainsi, les deux méthodes sont équivalentes en termes de grandeur
mesurée.
Les courants induits satisfont les équations de Maxwell, simplifiées selon des hypothèses d’homogénéité des conductivité, perméabilité et permittivité du matériau. Si une inhomogénéité comme une inclusion est présente, la conductivité électrique et/ou la perméabilité magnétique sont modifiées. D’après les équations 1.1 à 1.4, ceci entraîne une déviation des lignes des courants et par suite une variation du champ électromagnétique de réaction. En réalité, la grandeur d’intérêt est la variation de l’impédance ou de la transimpédance par rapport à sa valeur hors défaut. Soit, à la pulsation d’excitation ω
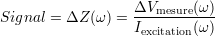
Ceci permet de détecter des défauts au sein de la pièce. Si le but du contrôle est l’estimation d’un paramètre constitutif de la pièce, il convient de réaliser un étalonnage de la sonde à l’aide de pièces étalons parfaitement connues ou de simulations numériques.
[Suivant] [Précédent] [Début] [Niveau supérieur]