3.1 Les représentations des signaux CF
Les signaux CF sont obtenus par balayage de la surface de la pièce. La sonde effectue de faibles
déplacements, suivant les deux axes 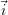 et
et 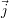 , définis à la section 2.4, du plan de la surface, de 100 μm dans le
cas des bobines micromoulées (décrites à la sous-section 2.2.2) ou de 200 μm dans le cas des microbobines CI
(décrites à la sous-section 2.2.1). À chaque position de la sonde, une mesure complexe de la transimpédance
de la sonde est réalisée, comme expliqué à la sous-section 1.3.1.2, c’est-à-dire le rapport en amplitude et en
phase de la tension de réception sur le courant d’émission. Une cartographie est ainsi constituée, appelée
« signal CF ». Cette cartographie de valeurs complexes est échantillonnée dans l’espace, avec un pas
correspondant aux distances de déplacement, pas ici relativement faible par rapport à la taille des
microbobines, d’un facteur de division respectif 10 ou 15 pour les bobines micromoulées ou les microbobines
CI.
, définis à la section 2.4, du plan de la surface, de 100 μm dans le
cas des bobines micromoulées (décrites à la sous-section 2.2.2) ou de 200 μm dans le cas des microbobines CI
(décrites à la sous-section 2.2.1). À chaque position de la sonde, une mesure complexe de la transimpédance
de la sonde est réalisée, comme expliqué à la sous-section 1.3.1.2, c’est-à-dire le rapport en amplitude et en
phase de la tension de réception sur le courant d’émission. Une cartographie est ainsi constituée, appelée
« signal CF ». Cette cartographie de valeurs complexes est échantillonnée dans l’espace, avec un pas
correspondant aux distances de déplacement, pas ici relativement faible par rapport à la taille des
microbobines, d’un facteur de division respectif 10 ou 15 pour les bobines micromoulées ou les microbobines
CI.
Cette section décrit les différentes représentations possibles pour des signaux CF. L’étude porte sur 30
défauts calibrés ; les acquisitions ont été faites par deux sondes comportant des microbobines de deux
technologies différentes, avec 5 stratégies d’émission-réception, pour une dizaine de fréquences différentes,
selon deux positionnements de la pièce (cf. ci-après, section 3.2). La base de données acquise compte environ
30 × 2 × 5 × 10 × 2 = 6000 signaux CF : il est à la fois inutile et impossible de tous les représenter. Les
figures suivantes montreront des exemples obtenus à partir d’un unique défaut, de dimensions
200 μm × 400 μm × 100 μm en profondeur×longueur×largeur. Ce défaut sera nommé ci-après défaut
« exemple ».
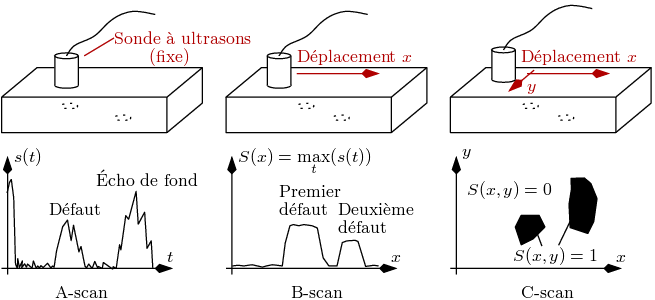
3.1.1 Une première représentation : le C-scan
3.1.1.1 Exemples de C-scan
Une première façon de visualiser les signaux CF mesurés est la représentation en tant que cartographie
complexe. Il s’agit, afin de prendre en compte la nature complexe du signal, d’un ensemble de deux images.
Elles affichent soit le couple module / argument, soit le couple partie réelle / partie imaginaire. Cette
représentation est souvent appelée C-scan (cf. encadré). Chaque image représente la valeur de la grandeur
correspondante suivant une échelle de couleurs qui peut être ou non notée à côté, continue ou discrète.
En général l’échelle de couleurs fait correspondre les valeurs par ordre croissant à une échelle
allant des couleurs froides aux couleurs chaudes, ou bien s’éclaircissant dans une même teinte.
Les axes des images sont les axes 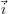 et
et 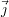 de balayage de la surface inspectée (vue suivant l’axe
de balayage de la surface inspectée (vue suivant l’axe
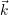 ).
).
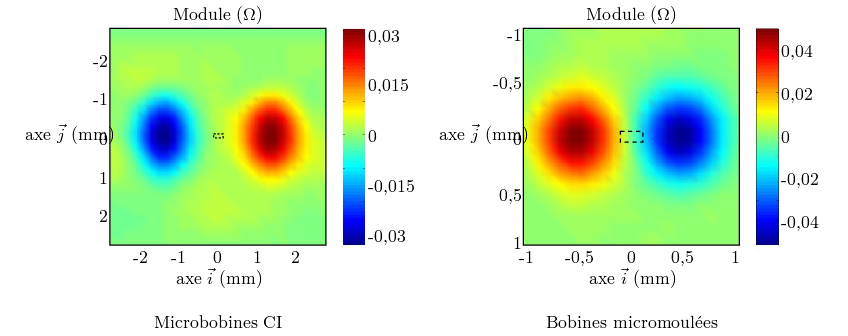
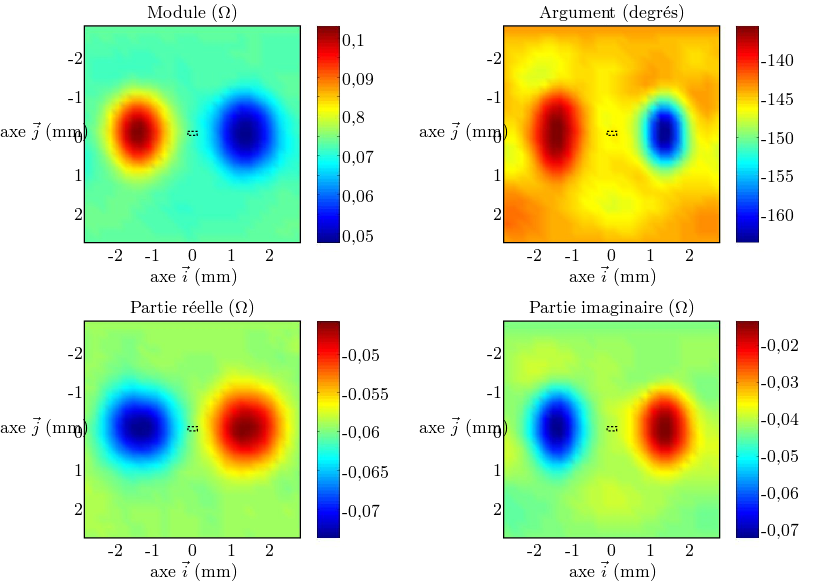
Les figures 3.2 et 3.3
montrent les signaux CF acquis autour du défaut « exemple » pour les deux technologies de
microbobines présentées aux sections 2.2.1 et 2.2.2. Ces acquisitions sont effectuées avec la
stratégie d’émission-réception ERE- et à une fréquence des courants d’émission de 4 MHz. Les
contours du défaut sont superposés en pointillés, à l’échelle. Chaque figure est composée de
quatre images, dont deux suffisent à représenter entièrement le signal CF. Le pas spatial de
balayage choisi est 200 μm dans le cas des microbobines CI et 100 μm dans le cas des bobines
micromoulées.
Malgré le caractère différentiel des mesures faites par la stratégie ERE- utilisée ici, la valeur du signal
CF loin du défaut n’est pas nulle. Des paramètres perturbateurs, comme les dissymétries entre les bobines ou
la connectique, engendrent aux fréquences de mesure (entre 1 et 10 MHz) des tensions très faibles qui,
divisées par la valeur du courant d’excitation lui aussi très faible, produisent cette valeur « à vide » non
nulle. Ceci engendre visuellement une différence très nette entre les modules des figures 3.2 et 3.3.
Cependant, cette valeur à vide est sans effet sur la suite des traitements, car retranchée juste après
l’acquisition.
3.1.1.2 Interprétation
La première chose remarquable à la vue de ces images est leur très faible correspondance avec la géométrie
du défaut. Le défaut originel, vu selon l’axe 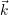 , a la forme d’un rectangle horizontal. Pourtant sur ces images,
ce sont deux lobes de forme ellipsoïdale qui sont visibles. De plus, la dimension des ellipses n’a aucun rapport
avec celle du défaut, car les acquisitions sur d’autres défauts donnent des lobes de dimensions similaires, mais
tend à se rapprocher davantage de la longueur du côté de chaque type de microbobine (environ 2,5 mm
pour les acquisitions issues des microbobines CI, environ 0,9 mm pour celles issues des bobines
micromoulées). Les zones contenant les lobes seront dans la suite nommées « zones de signal
utile ».
, a la forme d’un rectangle horizontal. Pourtant sur ces images,
ce sont deux lobes de forme ellipsoïdale qui sont visibles. De plus, la dimension des ellipses n’a aucun rapport
avec celle du défaut, car les acquisitions sur d’autres défauts donnent des lobes de dimensions similaires, mais
tend à se rapprocher davantage de la longueur du côté de chaque type de microbobine (environ 2,5 mm
pour les acquisitions issues des microbobines CI, environ 0,9 mm pour celles issues des bobines
micromoulées). Les zones contenant les lobes seront dans la suite nommées « zones de signal
utile ».
La présence de ces lobes signifie que le signal CF subit une variation non seulement lorsque le défaut est
situé sous le récepteur, mais aussi lorsqu’il est situé sous l’un des deux émetteurs. La figure 3.4 schématise
quelques positions des trois microbobines composant la sonde par rapport au défaut, pour quelques exemples
repérés sur un C-scan. Lorsque le défaut se situe sous la partie gauche de l’émetteur de droite (position a),
les lignes de courants induits de cet inducteur sont déviées vers la microbobine centrale de réception. Les
courants induits par l’inducteur de gauche ne sont par contre pas déviés, l’équilibre est rompu et la
tension aux bornes de la microbobine centrale n’est pas nulle. Si le défaut se trouve sous la
partie droite de la microbobine réceptrice (position b), une variation équivalente du signal CF est
observée, pour la même raison. Cette variation est située de part et d’autre de la frontière entre la
microbobine centrale et la microbobine de droite. Le maximum de cette variation est atteint
lorsque le défaut se situe entre les centres de chacune des deux microbobines (position c). Sur
la droite de symétrie de la sonde parallèle à l’axe 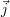 (positions d et e), l’influence du défaut
est identique pour les CF induits par les deux émetteurs et le signal CF est nul. Aux limites
des microbobines parallèlement à l’axe
(positions d et e), l’influence du défaut
est identique pour les CF induits par les deux émetteurs et le signal CF est nul. Aux limites
des microbobines parallèlement à l’axe 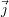 (position f ), le signal s’atténue très fortement, car les
déviations sont trop éloignés pour engendrer une variation importante de la tension aux bornes
de la microbobine de réception. Enfin, dans les parties externes des microbobines émettrices
(position g), les courants induits sont déviés vers l’extérieur de la sonde, ce qui ne produit aucun
signal.
(position f ), le signal s’atténue très fortement, car les
déviations sont trop éloignés pour engendrer une variation importante de la tension aux bornes
de la microbobine de réception. Enfin, dans les parties externes des microbobines émettrices
(position g), les courants induits sont déviés vers l’extérieur de la sonde, ce qui ne produit aucun
signal.
Ainsi, la zone d’influence du défaut est située autour des frontières entre chaque microbobine émettrice et
la microbobine réceptrice (et non uniquement la surface de la zone réceptrice comme il pourrait être
attendu). Ceci est une conséquence des petites dimensions des défauts considérés, comparativement à
celles des microbobines. Dans ce cas, les déviations des CF sont en effet localisées à l’endroit
où se trouve le défaut. Dans le cas d’un défaut de plusieurs millimètres de long, le C-scan CF
produit ressemble davantage à l’image géométrique du défaut, avec des bordures relativement
épaisses.
3.1.1.3 Traitement des images
L’influence des faibles dimensions des défauts peut aussi être expliquée par la théorie des filtres. En posant
ni et nj les indices des points de l’image selon les axes 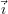 et
et 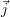 , il est possible de considérer la sonde comme un
filtre de traitement bidimensionnel discret
, il est possible de considérer la sonde comme un
filtre de traitement bidimensionnel discret
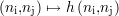
qui transforme une image binaire e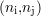 contenant le défaut vu selon l’axe
contenant le défaut vu selon l’axe 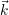 en l’image constituée par le
module du signal CF s
en l’image constituée par le
module du signal CF s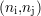 montrée par exemple dans les figures 3.2 ou 3.3. Un tel filtre
linéaire
permet alors d’écrire, sans prendre en compte le bruit extérieur
montrée par exemple dans les figures 3.2 ou 3.3. Un tel filtre
linéaire
permet alors d’écrire, sans prendre en compte le bruit extérieur
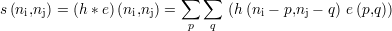 | (3.1) |
où * est l’opérateur de convolution. Il vient alors que les défauts dont les dimensions sont très faibles par
rapport à celles de la sonde constituent des impulsions de Dirac de l’ensemble des défauts, c’est à
dire des images d’entrée dont l’image de sortie correspondante est proportionnelle à la réponse
impulsionnelle du filtre h. Cela correspond bien à la ressemblance des réponses engendrées par tous ces
défauts.
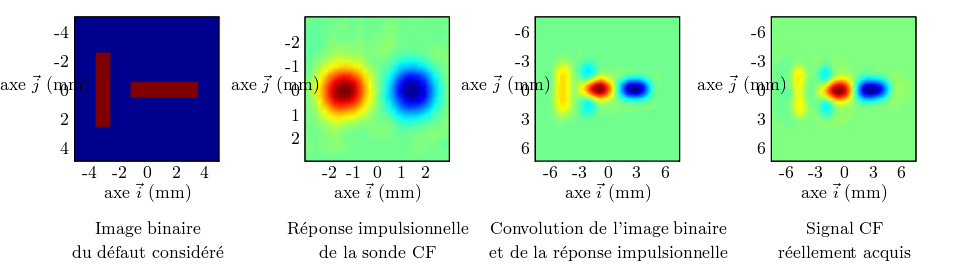
La réponse impulsionnelle de la sonde étant ainsi connue grâce à l’acquisition autour d’un
défaut de faibles dimensions, il est possible de calculer a priori ce que sera le signal CF pour
un défaut de taille importante grâce à la formule précédente. La figure 3.5 montre l’exemple
d’un défaut réellement évalué à l’aide de la sonde à microbobines CI et de la convolution de
l’image binaire du défaut par la réponse impulsionnelle de la sonde. Le défaut en question est
composé de deux fissures perpendiculaires de longueur 4,5 et 5 mm et de largeur 1 mm, espacées
par un isthme large de 1,5 mm : le défaut n’a pas une forme triviale. Cette convolution donne
une image assez proche de l’image correspondant au module du signal CF réellement obtenue :
les arêtes suivant l’axe 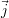 sont très visibles, tandis que les arêtes suivant l’axe
sont très visibles, tandis que les arêtes suivant l’axe 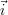 sont presque
invisibles. Seuls les contours des défauts peuvent être détectés, car la structure de la sonde est
différentielle.
sont presque
invisibles. Seuls les contours des défauts peuvent être détectés, car la structure de la sonde est
différentielle.
Ces signaux peuvent encore être utilisés à des fins de traitement du signal par les algorithmes d’inversion
ou de déconvolution. Ces algorithmes ont pour but de réaliser le traitement inverse de celui effectué par la
sonde, c’est-à-dire revenir à l’image originale du défaut. Il est souvent question d’utiliser la transformée
de Fourier discrète (TFD) de h, notée H. Cette matrice doit être inversée, et la transformée
inverse de Fourier de la matrice ainsi obtenue correspond au filtre inverse h-1. La matrice H est
rarement inversible, et plusieurs méthodes d’inversion approchée existent. Parmi ces méthodes se
trouvent
- le calcul de la matrice pseudo-inverse, obtenu par la fonction Matlab pinv à l’aide de la méthode
de Moore-Penrose[Moo20, Pen55], par décomposition en valeurs singulières ;
- le calcul du filtre inverse de Wiener[PAC90], qui fait intervenir les densités spectrales de puissance
(DSP) σB du bruit et σS du signal et qui s’écrit pour chaque couple de fréquences spatiales
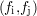
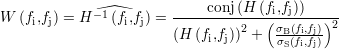
Il est par conséquent nécessaire d’évaluer ces DSP, c’est-à-dire souvent de les supposer a priori.
Ces deux méthodes ont été mises en œuvre sur les acquisitions effectuées. Les faibles dimensions des
défauts considérés ont eu pour conséquence des résultats peu concluants. Néanmoins, trois observations ont
pu être dégagées au sujet de ces deux méthodes :
- Elles donnent des résultats assez proches. Si les DSP dans l’expression du filtre de Wiener sont
correctement estimées, le résultat de cette méthode de déconvolution est normalement meilleur,
en termes de rapport signal sur bruit, car la pseudo-inversion produit une amplification du bruit
due à l’inversion des plus faibles valeurs singulières de H.
- Le calcul de la pseudo-inverse devient extrêmement coûteux en temps de calcul lorsque la taille
de h devient importante. Ce n’est pas le cas du filtre de Wiener, qui est un simple calcul point
par point de matrices.
- En termes de simplicité de mise en œuvre, le filtre de Wiener a l’inconvénient majeur de ne pas
être universel : au contraire de la matrice de Moore-Penrose, il faut le recalculer pour chaque
image s. De plus, le réglage consistant à l’estimation des DSP est relativement sensible. Si la
quantité σB∕σS déterminée est trop faible, le résultat n’est que très peu amélioré par rapport
à la pseudo-inversion. Si la quantité σB∕σS déterminée est surestimée, l’apparition de lobes
secondaires latéraux constitue une baisse sensible de la qualité de déconvolution.
En conclusion, cette approche linéaire permet dans certains cas de proposer efficacement des
prétraitements de déconvolution favorisant l’interprétabilité des images CF, mais reste dans le cas général
insuffisante pour la caractérisation quantitative des défauts. Il faut alors mettre en œuvre des modèles
inverse plus élaborés, qui font actuellement l’objet d’une recherche active.
3.1.2 Une deuxième représentation : la signature complexe
Une deuxième représentation des signaux CF est très utilisée dans le domaine du CND par CF. Il s’agit de la
représentation dans le plan complexe de chaque valeur mesurée de la transimpédance. L’abscisse
et l’ordonnée correspondent respectivement aux parties réelle et imaginaire de cette grandeur
complexe.
Lorsque l’évaluation est effectuée le long d’une ligne uniquement, évaluation qui peut être représentée
sous forme de B-scan, il est d’usage de relier les points de mesure entre eux, afin de garder une information
spatiale sur l’ordre des points complexes. Ce genre de graphe est alors appelé courbe ou figure de Lissajous.
Dans le cas des acquisitions effectuées ici, il est préférable de ne pas lier les points entre eux, afin de
garder une certaine lisibilité des graphes. La figure 3.6 montre les signatures obtenues pour le
défaut « exemple » avec les deux technologies de microbobines. Chaque croix correspond à un
point de mesure (les points de mesure sont espacés sur les deux axes 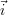 et
et 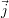 de 200 μm pour
les acquisitions faites avec la sonde à microbobines CI et de 100 μm dans le cas des bobines
micromoulées).
de 200 μm pour
les acquisitions faites avec la sonde à microbobines CI et de 100 μm dans le cas des bobines
micromoulées).
Sur chacune de ces deux signatures, les points centraux correspondent aux mesures hors
de la zone de signal utile, loin du défaut. Comme avec la représentation C-scan, cette valeur
centrale moyenne est non nulle. Une variation complexe constituée d’un grand nombre de points,
symétrique de part et d’autre de cette valeur moyenne, correspond aux lobes des figures 3.2 et
3.3.
Malgré la perte des informations spatiales comme la forme du signal utile, cette représentation offre des nouvelles
informations. En particulier, elle permet de mieux visualiser les tendances générales de variation de l’impédance
de la sonde, en module et en phase. Ce mode de représentation est souvent choisi comme point de départ pour
paramétriser
l’acquisition, c’est-à-dire réduire à quelques valeurs une signature CF entière[KSK+04]. Une paramétrisation
des signatures CF est par exemple l’objet du chapitre 5. Elle y sert à obtenir les dimensions des défauts
détectés.
3.1.3 Une (presque-)troisième représentation : l’amplitude principale
3.1.3.1 Intérêt de la transformation
La dernière possibilité pour la représentation des signaux CF n’en est pas vraiment une. Il s’agit des mesures
complexes, projetées sur l’axe de plus grande variation de la signature CF et représentées en tant qu’image
spatiale. Cela reste une sorte de C-scan, appelée par la suite « image CF ».
L’intérêt de cette représentation est de simplifier la visualisation des images CF des défauts, au prix
d’une perte si possible minime d’informations. En effet, comme cela est visible sur les figures 3.2 et 3.3, se
contenter d’une image unique par signal CF signifie nécessairement faire un choix entre module, partie réelle
et partie imaginaire. Choisir le module pose le problème de l’opposition des valeurs des deux lobes : le module
étant toujours positif, l’opposition ne peut être conservée. Les deux dernières grandeurs ne sont pas
préférables l’une à l’autre et il est par conséquent difficile d’en choisir arbitrairement une. La plus
intéressante des deux serait, d’après les signatures CF des figures 3.6-a et 3.6-b, plutôt la partie imaginaire
pour la première, plutôt la partie réelle pour la seconde. L’idée est alors de choisir une combinaison linéaire
des deux, qui maximise l’énergie du signal CF conservée. Plusieurs techniques existent pour ce
faire.
3.1.3.2 Première méthode : l’analyse en composantes principales
Le terme « amplitude principale » peut être rapporté à la méthode de l’analyse en composantes principales
(ACP), qui effectue une comparaison des différentes composantes d’un signal, après projection dans un
sous-espace de représentation engendré par une nouvelle base orthogonale[Sap78, MKB79]. Cette base
orthogonale peut être indifféremment déterminée à l’aide de la décomposition en valeurs singulières[Bjo96]
de la matrice de covariance des deux vecteurs partie réelle et partie imaginaire, ou de la matrice
dont les colonnes sont ces deux vecteurs. L’effet produit est la maximisation des projections
orthogonales des points sur chacun des axes définis. La première composante produite par l’ACP est
a priori l’amplitude principale recherchée, du moins pour le type de signaux CF considérés
ici.
3.1.3.3 Deuxième méthode : l’estimateur des moindres carrés ordinaires
Une autre méthode est le calcul de l’estimateur des moindres carrés ordinaires (EMCO). Cette
méthode permet de minimiser la somme des carrés des erreurs entre les valeurs mesurées et les
valeurs estimées[VHV91]. Il s’agit souvent de mesures y réalisées pour un paramètre de mesure x
connu : le but est alors de minimiser l’erreur ŷ - y d’estimation. Ces erreurs sont par conséquent
les distances verticales entre les points de mesure et la droite trouvée, comme indiqué par la
figure 3.7-a.
Dans le cas de cette étude, l’utilisation de l’EMCO est sensiblement différente, car le but est de
déterminer l’existence d’une relation entre deux grandeurs mesurées. Il n’y a aucune légitimité à donner un
sens physique différent aux parties réelle ou imaginaire de l’impédance, qui jouent respectivement le rôle de x
et y. Il convient donc de minimiser ici la distance orthogonale à la droite recherchée, comme le montre la
figure 3.7-b.
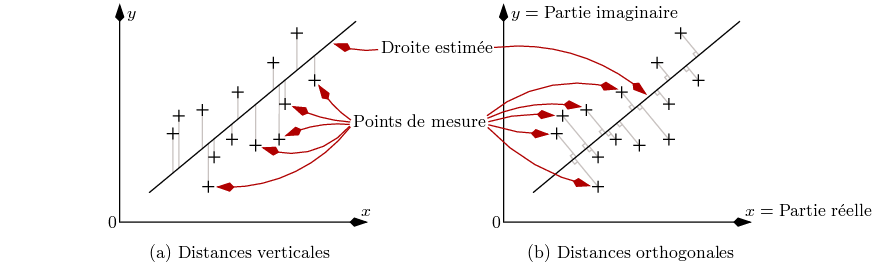
Le calcul de cette droite prend en compte les n points de mesure de coordonnées (xi,yi). La moyenne des
x, la variance des x et la covariance des (x,y) sont respectivement notées
Pour une droite affine quelconque, d’équation
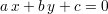 | (3.2) |
où a, b et c sont les paramètres à déterminer, la distance algébrique depuis un point de coordonnées (xi,yi)
est définie par
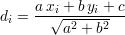 | (3.3) |
La somme des carrés des distances entre les n points de mesure et la droite s’écrit
Sa dérivée partielle par rapport à c vaut
![[ ]
∂Σ 2 ∑n
∂c-= a2 +-b2 (axi + byi)+ n c
i=1](memoire114x.png)
et s’annule si et seulement si
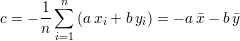
Cela signifie que la droite minimisant l’erreur orthogonale passe par le barycentre (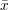 ,
,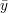 ) de l’ensemble des
points de mesure. Après substitution, la somme à minimiser s’écrit
) de l’ensemble des
points de mesure. Après substitution, la somme à minimiser s’écrit
Pour minimiser cette somme, ses dérivées partielles par rapport à a et b sont calculées :L’annulation de ces deux dérivées engendre la même équation
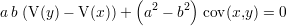 | (3.5) |
En fixant b, il est possible de calculer la valeur de a par la résolution de l’équation du second
degré,
soit
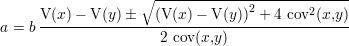
La symétrie de l’équation 3.5 donne au calcul équivalent pour b en fixant a un résultat identique. Il est
alors envisageable de choisir, par exemple, d’avoir un couple (a,b) normalisé tel que
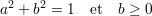
Les deux solutions trouvées correspondent à deux extrema de la somme S. La solution minimale correspond
à une dérivée seconde de S par rapport à a positive. La valeur de cette dérivée seconde, lorsque la dérivée
première s’annule, est positive si et seulement si
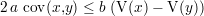
Cette inéquation permet de choisir la solution correcte, qui est
ce qui conduit à la solution
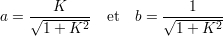
qui peut être simplifiée
en
L’amplitude principale s′ est l’abscisse de la projection de chaque point de mesure sur la droite
déterminée. Cette projection orthogonale s’écrit, à une constante additive près
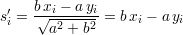
3.1.3.4 Troisième méthode : le maximum de vraisemblance
Une troisième méthode est celle du maximum de vraisemblance. Il y est question de déterminer les
paramètres d’une loi de distribution afin de l’optimiser pour l’ensemble des échantillons mesurés[Rao65]. En
pratique, il faut trouver une variable aléatoire fonction des mesures effectuées, dont la loi de
distribution dépend des paramètres recherchés. Le choix des paramètres est effectué grâce à la
maximisation de la vraisemblance qui prend en compte l’ensemble des probabilités pour chacune des
mesures.
Ici, les paramètres recherchés sont les coefficients a, b et c de la droite d’équation 3.2. La variable
aléatoire choisie est la distance algébrique di définie par l’équation 3.3. Cette distance équivaut à l’erreur
commise. Si la distribution de cette variable aléatoire est posée, par hypothèse, comme étant une loi normale
centrée et d’écart-type σ, la densité de probabilité de di s’exprime
En supposant l’indépendance entre les différents échantillons, la vraisemblance est par définition
le produit de l’ensemble des n densités de la variable aléatoire prise pour chaque échantillon,
soit
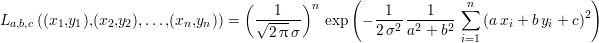
Trouver les paramètres a, b et c qui maximisent cette quantité n’est pas chose aisée. Cependant, il est
possible d’obtenir les mêmes paramètres en utilisant la fonction logarithme népérien ln. En effet, La,b,c est
strictement positive et ln est croissante et monotone. Il vient
où Σ(a,b,c) est la somme des distances carrées minimisée précédemment pour le calcul de l’EMCO. Il
apparaît clair que maximiser la quantité ln 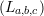 en fonction de a, b et c revient exactement à minimiser
Σ(a,b,c). La méthode du maximum de vraisemblance donne, dans le cas étudié, le même résultat que le
calcul de l’EMCO.
en fonction de a, b et c revient exactement à minimiser
Σ(a,b,c). La méthode du maximum de vraisemblance donne, dans le cas étudié, le même résultat que le
calcul de l’EMCO.
3.1.3.5 Mise en œuvre
Les résultats donnés par les deux méthodes de calcul (ACP et EMCO) sont numériquement rigoureusement
identiques. Ceci est dû à l’utilisation dans le calcul de l’ACP de la covariance des données. Le calcul de
l’EMCO faisant lui aussi intervenir les variances et covariances des parties réelles x et imaginaires y, les deux
calculs ont un fondement théorique différent mais une mise en œuvre similaire et donnant par conséquent le
même résultat.
Une image unique est obtenue, qui maintient la visualisation de la forme géométrique des signaux CF.
Les amplitudes principales correspondant au défaut « exemple » sont représentées dans la figure 3.8. La
dynamique de ces grandeurs, c’est-à-dire la différence entre les valeurs extrêmes, visible sur les échelles de
couleurs, est bien maximisée.
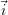 et
et 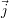 , définis à la section 2.4, du plan de la surface, de 100 μm dans le
cas des bobines micromoulées (décrites à la sous-section 2.2.2) ou de 200 μm dans le cas des microbobines CI
(décrites à la sous-section 2.2.1). À chaque position de la sonde, une mesure complexe de la transimpédance
de la sonde est réalisée, comme expliqué à la sous-section 1.3.1.2, c’est-à-dire le rapport en amplitude et en
phase de la tension de réception sur le courant d’émission. Une cartographie est ainsi constituée, appelée
« signal CF ». Cette cartographie de valeurs complexes est échantillonnée dans l’espace, avec un pas
correspondant aux distances de déplacement, pas ici relativement faible par rapport à la taille des
microbobines, d’un facteur de division respectif 10 ou 15 pour les bobines micromoulées ou les microbobines
CI.
, définis à la section 2.4, du plan de la surface, de 100 μm dans le
cas des bobines micromoulées (décrites à la sous-section 2.2.2) ou de 200 μm dans le cas des microbobines CI
(décrites à la sous-section 2.2.1). À chaque position de la sonde, une mesure complexe de la transimpédance
de la sonde est réalisée, comme expliqué à la sous-section 1.3.1.2, c’est-à-dire le rapport en amplitude et en
phase de la tension de réception sur le courant d’émission. Une cartographie est ainsi constituée, appelée
« signal CF ». Cette cartographie de valeurs complexes est échantillonnée dans l’espace, avec un pas
correspondant aux distances de déplacement, pas ici relativement faible par rapport à la taille des
microbobines, d’un facteur de division respectif 10 ou 15 pour les bobines micromoulées ou les microbobines
CI.
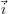 et
et 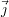 de balayage de la surface inspectée (vue suivant l’axe
de balayage de la surface inspectée (vue suivant l’axe
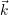 ).
).
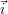 , d’une
profondeur de
, d’une
profondeur de 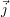 (superposé en pointillés)
(superposé en pointillés)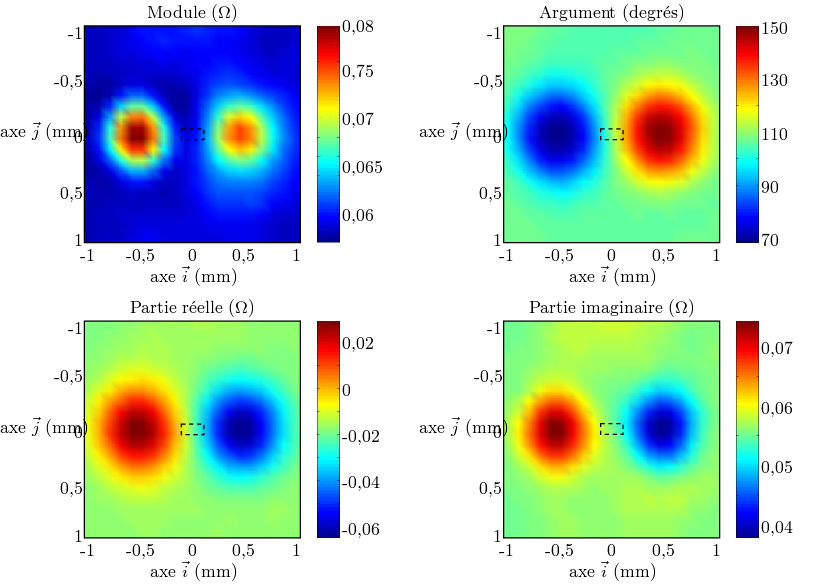
 , d’une
profondeur de
, d’une
profondeur de  (superposé en pointillés)
(superposé en pointillés) , a la forme d’un rectangle horizontal. Pourtant sur ces images,
ce sont deux lobes de forme ellipsoïdale qui sont visibles. De plus, la dimension des ellipses n’a aucun rapport
avec celle du défaut, car les acquisitions sur d’autres défauts donnent des lobes de dimensions similaires, mais
tend à se rapprocher davantage de la longueur du côté de chaque type de microbobine (environ
, a la forme d’un rectangle horizontal. Pourtant sur ces images,
ce sont deux lobes de forme ellipsoïdale qui sont visibles. De plus, la dimension des ellipses n’a aucun rapport
avec celle du défaut, car les acquisitions sur d’autres défauts donnent des lobes de dimensions similaires, mais
tend à se rapprocher davantage de la longueur du côté de chaque type de microbobine (environ  (positions
(positions  (position
(position 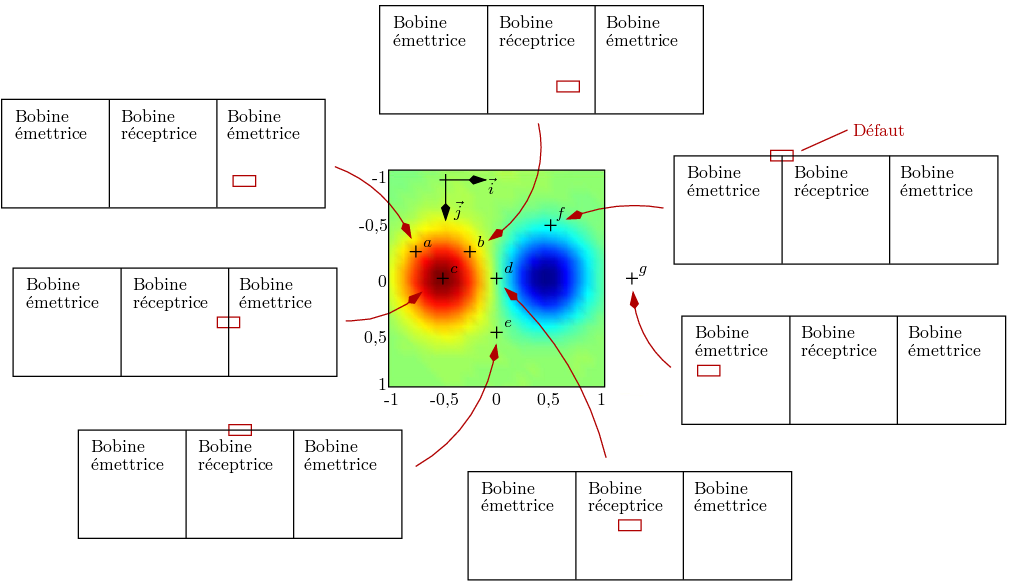
 et
et 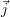 , il est possible de considérer la sonde comme un
filtre de traitement bidimensionnel discret
, il est possible de considérer la sonde comme un
filtre de traitement bidimensionnel discret
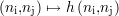
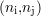 contenant le défaut vu selon l’axe
contenant le défaut vu selon l’axe 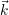 en l’image constituée par le
module du signal CF
en l’image constituée par le
module du signal CF 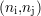 montrée par exemple dans les figures
montrée par exemple dans les figures 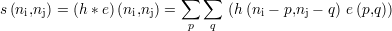
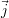 sont très visibles, tandis que les arêtes suivant l’axe
sont très visibles, tandis que les arêtes suivant l’axe 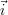 sont presque
invisibles. Seuls les contours des défauts peuvent être détectés, car la structure de la sonde est
différentielle.
sont presque
invisibles. Seuls les contours des défauts peuvent être détectés, car la structure de la sonde est
différentielle.
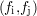
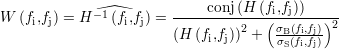
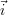 et
et 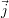 de
de 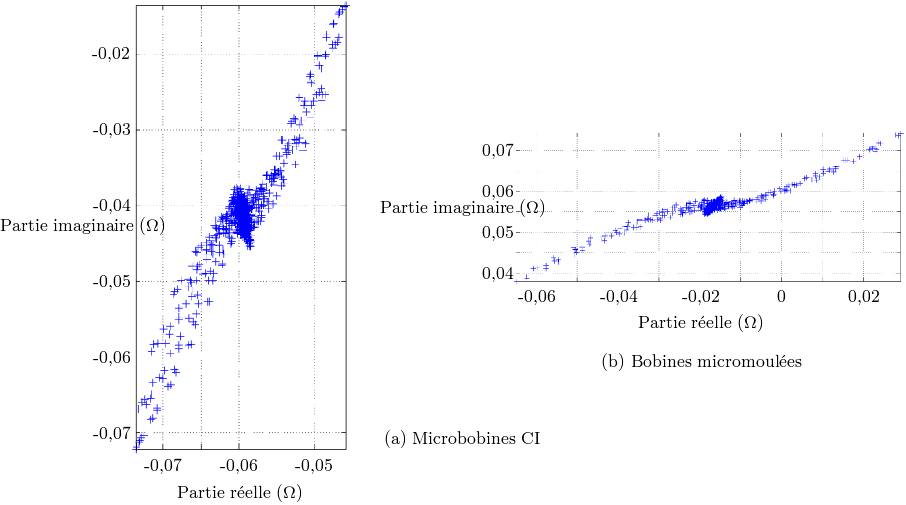
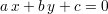
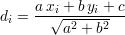
![1 ∑n
Σ(a,b,c) = --2---2 (a xi + byi + c)2
a + b i=1
1 [ ∑n n∑ ]
= --2---2 (axi + byi)2 + 2 (a xi + b yi) c+ n c2
a + b i=1 i=1](memoire113x.png)
![[ ]
∂Σ 2 ∑n
∂c-= a2 +-b2 (axi + byi)+ n c
i=1](memoire114x.png)
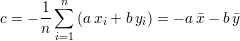
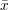
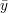
![[ n ]
Σ(a,b) = ---1--- ∑ (a (x - x¯)+ b (y - ¯y))2
a2 + b2 i i
[ i=1 n n n ]
= ---1--- a2∑ (x - ¯x)2 + b2 ∑ (y - ¯y)2 + 2a b∑ (x - ¯x)(y - ¯y)
a2 + b2 i=1 i i=1 i i=1 i i
n ( 2 2 )
= a2-+-b2 a V (x )+ b V (y)+ 2 ab cov(x,y) (3.4)](memoire118x.png)
![∂ Σ n [ 2 ( 3 2 ) ]
∂a- = --2---2-2 2ab (V(x) - V(y))+ 2 b - a b cov (x,y)
(a + b ) [ ( ) ]
∂-Σ = ----n---- 2a2b (V(y)- V(x))+ 2 a3 - ab2 cov(x,y)
∂b (a2 + b2)2](memoire119x.png)
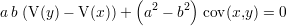
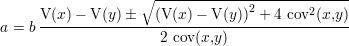
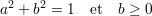
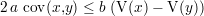
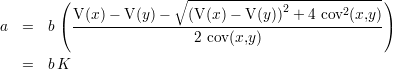
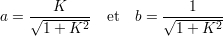
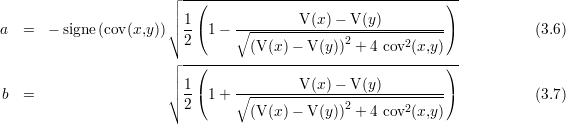
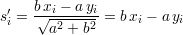
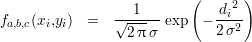
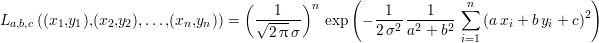
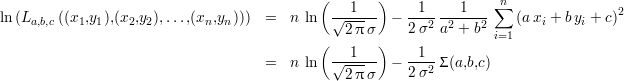
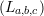 en fonction de
en fonction de