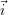 ou
ou 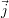 ;
;
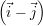 ou
ou 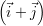 ;
;
[Suivant] [Précédent] [Fin] [Niveau supérieur]
La méthode d’inversion choisie est une méthode directe, non itérative. Cette méthode permet une mise en œuvre rapide, avec un pré-réglage des coefficients grâce à des données a priori. Elle nécessite cependant l’établissement d’un modèle inverse, ce qui n’est pas toujours possible. Pour cette étude, un tel modèle a pu être défini. Cette section explique en détail les différentes étapes ayant permis la réalisation de l’algorithme d’inversion : la définition des caractéristiques des défauts à estimer et des paramètres des signaux CF, l’obtention du modèle inverse, les améliorations apportées grâce aux informations a priori et les réglages des coefficients du modèle.
Les défauts considérés dans ces travaux sont des fissures parallélépipédiques. Ils ont donc trois dimensions :
Dans cette étude, la largeur des défauts est exclue des dimensions à estimer, car l’ensemble des défauts à disposition ne permet pas de connaître son influence sur les signaux CF. Les seules dimensions à estimer sont la longueur et la profondeur.
L’orientation est aussi une caractéristique importante influençant les signaux CF. Ici, les acquisitions ont été faites à partir de quatre orientations différentes. Il sera par conséquent impossible de déterminer de façon continue un angle entre les orientations principales du défaut et de la sonde, mais il sera question d’un choix entre les trois cas suivants :
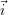 ou
ou 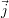 ;
;
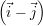 ou
ou 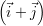 ;
;
Chaque défaut détecté doit être classé au sein de l’un de ces trois cas6 : il s’agit d’une classification.
Pour chaque jeu de conditions de mesure, c’est-à-dire pour chaque triplet constitué d’une technologie de microbobines, d’une stratégie d’émission-réception et d’une fréquence des courants d’excitation, 60 acquisitions sont effectuées, 90 signaux CF sont disponibles après combinaison. Cela correspond à 30 défauts différents, parmi lesquels chaque valeur de longueur se rapporte à 6 défauts et chaque valeur de profondeur à 10 défauts. Concernant les orientations, si o1 et o2 correspondent chacune à 12 défauts, o3 n’est l’orientation que de 6 défauts.
Ces paramètres sont assez nombreux et redondants. Le bruit que chacun d’eux comporte individuellement et de façon aléatoire risque de rendre instable le processus d’inversion. Il faut sélectionner les plus pertinents. Deux axes de sélection doivent être privilégiés :
Parmi les paramètres calculés à partir des trois signaux CF correspondant à un même défaut, deux paramètres apparaissent comme particulièrement intéressants pour l’estimation de l’orientation, effectuée à la sous-section 5.4.3.
Le premier de ces deux paramètres est la différence entre les dynamiques des deux premiers modes, divisée par la dynamique du mode combiné. Ce rapport s’écrit
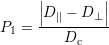
Le second de ces deux paramètres est le rapport entre l’angle d’inclinaison et la dynamique du mode combiné, donné par
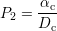
Ces paramètres présentent l’avantage de varier fortement en fonction de l’orientation des défauts et faiblement en fonction des autres caractéristiques.
Afin d’effectuer un premier tri parmi les paramètres choisis, une méthode simple peut être d’effectuer une étude de corrélation entre les paramètres des signaux CF et les différentes caractéristiques pour l’ensemble des défauts. Une étude de corrélation est la recherche des ressemblances dans les variations des données. Cette étude est menée par le calcul du coefficient de corrélation linéaire qui s’écrit
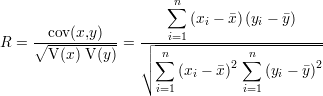
avec les xi et yi les n réalisations des grandeurs x et y.
La figure 5.5 montre les résultats de cette étude. Le produit ℓ × p a été ajouté au sein des caractéristiques, pour essayer de trouver l’existence de relations affines avec cette quantité. Il apparaît dans ces valeurs que les angles d’inclinaison des signatures CF ont une forte corrélation avec la profondeur ; les dynamiques, qu’elles soient principales ou secondaires, sont fortement corrélées avec le produit ℓ × p.
|
|
La première corrélation s’explique essentiellement par l’équation 1.5. Elle montre en effet que le déphasage de la densité des courants induits au sein de la pièce testée dépend de façon importante de la profondeur à laquelle ils se situent au sein de cette pièce. La variation de l’angle d’inclinaison est la variation du déphasage entre la tension mesurée et le courant d’excitation, donc la variation de phase de la tension mesurée. La tension mesurée étant modifiée lorsque les courants induits sont déviés, l’angle d’inclinaison de la signature CF observée est par conséquent fonction de la profondeur p du défaut.
Pour la deuxième corrélation, il convient de restreindre l’analyse au cas présent des défauts de type parallélépipèdes plats, avec une largeur plus faible que la longueur. Il a été montré dans ce cas que la largeur des fissures a une influence négligeable sur le champ magnétique de réaction dû aux défauts : les signaux, en particulier en amplitude, sont très influencés par la surface latérale des défauts. Cette propriété est d’ailleurs à la base de la modélisation par éléments finis de défauts fins[CSLBM07b], les défauts étant modélisés comme des fissures infiniment plates. Cette propriété est ici retrouvée par l’étude des coefficients de corrélation linéaire.
Discussion sur l’utilisation des coefficients de corrélation linéaire
Il est couramment admis que R quantifie la corrélation linéaire entre deux données, c’est-à-dire la
possibilité de trouver une relation affine entre ces deux vecteurs. Toute autre relation n’est pas prise en
compte : par exemple, une relation polynomiale d’ordre 2 donne en général un coefficient de corrélation
linéaire très faible. De plus, ce coefficient est très sensible aux valeurs extrêmes, comme le montre la
figure 5.6. Elle présente quatre couples de vecteurs possédant les mêmes moyennes, variances, coefficients de
corrélation linéaire et droites de régression linéaire, malgré une différence visuelle très importante. Ces
quatre couples, connus sous le nom du quartet d’Anscombe, ont été publiés par F. Anscombe en
1973[Ans73].
|
|
Néanmoins, calculer les coefficients de corrélation linéaire entre les paramètres des signaux CF acquis et les caractéristiques des défauts inspectés permet d’obtenir des informations intéressantes, dans le cas où des relations affines existent. Par exemple, la longueur et la profondeur n’offrent, pour aucun des paramètres, une corrélation très importante. Il n’y a a priori que peu de chances de pouvoir définir une relation linéaire entre chacun des paramètres et ces caractéristiques. Il est par contre tout à fait envisageable que des relations non linéaires existent.
L’inversion envisagée doit permettre de retrouver à partir d’un signal CF paramétré les caractéristiques du défaut inspecté. Les processus de décimation et de suréchantillonnage des signaux CF acquis, présentés aux sections 3.4 et 3.5 correspondent au processus d’échantillonnage spatial que réaliserait une acquisition « réaliste ». Le pas d’échantillonnage spatial du signal CF après décimation est égal au pas original (100 μm) multiplié par le facteur de décimation nd. Ce processus de décimation introduit le fait que ces contrôles effectués en pratique contiennent moins de points de mesure et par conséquent moins d’informations : plus le pas d’échantillonnage spatial ou le facteur de décimation est important, plus la dynamique, le RSB et la probabilité de détection sont détériorés. Il est nécessaire que les valeurs des paramètres utilisés au sein de l’inversion soient le moins possible affectées par la décimation ou la variation du pas d’échantillonnage spatial.
Les figures 5.7 et 5.8 montrent l’évolution des coefficients de corrélation en fonction du facteur de décimation, plus précisément pour un facteur nd = 5 à la première et nd = 10 à la deuxième figure. Le cas nd = 5 correspond à un pas d’échantillonnage spatial égal à 500 μm, soit la moitié de la largeur d’une microbobine ; le cas nd = 10 correspond à un pas d’échantillonnage spatial égal à 1 mm, soit la largeur d’une microbobine. Elles indiquent que la corrélation entre les angles d’inclinaison des signatures CF et les profondeurs des défauts, conservées encore pour nd = 5, sont très dégradées à nd = 10. Au contraire, les valeurs des coefficients de corrélation linéaire entre les dynamiques et les surfaces latérales des défauts sont assez stables.
|
|
|
|
Le mode combiné correspond à un signal CF identique pour deux défauts perpendiculaires entre eux. Il est ainsi souvent préférable d’utiliser les paramètres calculés sur les signatures CF combinées. En effet, la dynamique du mode combiné est par exemple identique pour ces deux défauts perpendiculaires, contrairement aux modes parallèle et perpendiculaire. Elle ne dépend que des autres caractéristiques des défauts.
Dans le cas de l’étude menée ici, estimer l’orientation des défauts détectés correspond, contrairement à l’estimation de leur profondeur et de leur longueur, à une classification entre trois classes définies à la sous-section 5.4.1. Les deux paramètres P1 et P2 ont été définis à la sous-section 5.4.2.1 et choisis pour réaliser cette estimation. Il s’agit de paramètres faisant intervenir plusieurs paramètres élémentaires des signatures CF. Ils ont été déterminés grâce à l’observation de leur évolution en fonction des caractéristiques des défauts inspectés7, représentée à la figure 5.9 pour un exemple des 30 combinaisons de signaux CF, acquis avec la sonde à bobines micromoulées, la stratégie d’émission-réception ERE- et une fréquence des courants d’excitation égale à 5 MHz.
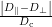
Le paramètre P1 réalise le rapport entre, d’une part la différence entre les dynamiques des deux modes parallèles et perpendiculaires, d’autre part la dynamique du mode combiné. Cette dernière étant nécessairement plus grande que les dynamiques non combinées, ce rapport est donc normalisé et toujours compris entre 0 et 1. Lorsque l’une des deux sondes est privilégiée, c’est-à-dire possède une orientation principale proche de celle du défaut, la combinaison des signaux CF devient semblable au signal CF de la sonde privilégiée : ce rapport est alors proche de 1. Dans le cas contraire et plus particulièrement lorsque l’orientation du défaut est située à 45˚ de chacune des deux sondes, ce rapport est normalement proche de 0, car les deux signaux non combinés et donc les dynamiques D∥ et D⊥ sont comparables.
La figure 5.9-a, représente l’évolution du paramètre P1 et montre qu’il est possible d’identifier aisément l’orientation o1. En effet, une valeur de séparation fixée à 0,4 donne de bons résultats expérimentaux. Cependant, l’utilisation unique de ce paramètre ne permet pas de différencier les défauts d’orientation o2 et o3.
Il a été observé (cf. la sous-section suivante) que la dynamique et l’angle d’inclinaison des signatures CF varient de façon affine en fonction de la profondeur p et de ℓ. Leurs évolutions ne sont pas identiques. En particulier, si l’évolution en fonction de p pour ℓ fixée est une fonction affine croissante dans les deux cas, l’évolution en fonction de ℓ pour p fixée est une fonction affine, respectivement décroissante et croissante dans le cas de αc et de Dc. L’idée est alors que le rapport αc∕Dc a le double intérêt d’être faiblement influencé par p et fortement par ℓ. Les sens de variation de αc, Dc et P2 sont résumés par le tableau 5.1.
|
L’évolution du paramètre P2 sur la figure 5.9-b montre qu’une valeur importante de ce paramètre correspond à une longueur faible, indépendamment de la profondeur du défaut. À largeur fixe, cela signifie qu’au-delà d’un seuil de séparation, le paramètre P2 indique que le défaut possède une surface débouchante carrée, sans orientation principale.
Il est ainsi possible grâce à ce deuxième paramètre de déterminer si la classe de l’orientation du défaut détecté est o3 ou non. Une valeur de séparation peut donc être préalablement établie uniquement en fonction des conditions de mesure.
Une fois l’orientation détectée, la profondeur et la longueur peuvent à leur tour être estimées. Cette fois, il ne s’agit pas d’une classification mais d’une estimation continue. Les profondeurs et longueurs estimées peuvent prendre un nombre infini de valeurs au sein d’une plage réaliste.
Pour ce faire, l’angle d’inclinaison ainsi que la dynamique des signatures CF combinées sont utilisés. Leur évolution en fonction des caractéristiques des défauts est représentée à la figure 5.10, dans les mêmes conditions que celles de la figure 5.9. Ces évolutions ont en commun qu’une valeur de paramètre ne correspond pas à une valeur unique des caractéristiques des défauts inspectés. Il n’est donc pas possible de déterminer la profondeur ou la longueur uniquement à partir d’un seul de ces deux paramètres. Il est néanmoins possible d’établir un modèle inverse à partir de l’ensemble de ces deux paramètres.
L’évolution en « dents de scie » de l’angle d’inclinaison αc est en réalité une fonction bilinéaire à deux
variables, affine pour chacune des deux variables. En effet, la figure 5.11-a montre que pour une valeur de ℓ
fixée, la variation de αc est une fonction affine de p. La figure 5.11-b montre que pour une valeur de p fixée,
la variation de αc est aussi une fonction affine de ℓ. Les droites d’équation αc ℓ=cste = fℓ(p) ont toutes la
même origine et une pente qui dépend de la valeur de ℓ. Les droites d’équation αc
ℓ=cste = fℓ(p) ont toutes la
même origine et une pente qui dépend de la valeur de ℓ. Les droites d’équation αc p=cste = gp(ℓ)
ont elles une pente et une origine dépendant de la valeur de p. Il est par conséquent possible
d’écrire
p=cste = gp(ℓ)
ont elles une pente et une origine dépendant de la valeur de p. Il est par conséquent possible
d’écrire
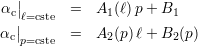
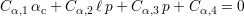 | (5.1) |
L’évolution de la dynamique principale des signatures CF est présentée à la figure 5.12. Ici aussi, il est
possible de trouver des relations affines à coefficients variables entre la dynamique et chacune des deux
dimensions des défauts inspectés. De même que pour l’angle d’inclinaison, les droites d’équation
Dc ℓ=cste = fℓ′(p) ont toutes la même origine et une pente qui dépend de la valeur de ℓ ; les droites
d’équation Dc
ℓ=cste = fℓ′(p) ont toutes la même origine et une pente qui dépend de la valeur de ℓ ; les droites
d’équation Dc p=cste = gp′(ℓ) ont elles une pente et une origine dépendant de la valeur de p. Il est encore une
fois possible d’écrire
p=cste = gp′(ℓ) ont elles une pente et une origine dépendant de la valeur de p. Il est encore une
fois possible d’écrire
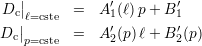
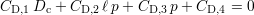 | (5.2) |
La dynamique secondaire dc est également exploitable à la place de la dynamique principale. Le modèle à adopter serait équivalent au précédent. La similarité des évolutions respectives de ces deux paramètres entraîne que leur utilisation simultanée n’améliore pas significativement les résultats des estimations. De plus, la dynamique secondaire est moins robuste que la dynamique principale vis-à-vis du facteur de décimation : les résultats des estimations à partir de la dynamique secondaire sont plus rapidement dégradés. Par conséquent, seuls la dynamique principale et l’angle d’inclinaison ont été choisis pour être utilisés dans l’algorithme d’inversion.
Les équations 5.1 et 5.2 constituent un système de deux équations non linéaires à deux inconnues, pour des valeurs de αc et Dc déterminées par la paramétrisation de la signature CF considérée. Les équations, d’origine différentes, sont indépendantes entre elles : ce système est a priori inversible.
Le modèle inverse est obtenu par l’inversion de ce système. Il vient, par élimination des termes en p × ℓ
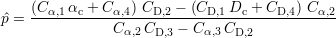 | (5.3) |
Cette expression montre la relation affine existant entre 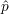 et les paramètres αc et Dc, les coefficients étant
constants. Il est donc équivalent d’écrire
et les paramètres αc et Dc, les coefficients étant
constants. Il est donc équivalent d’écrire
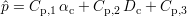 | (5.4) |
Par factorisation des p et division membre à membre des deux équations du système, il vient une relation définissant la longueur estimée en fonction des paramètres
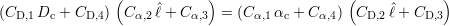
ou encore
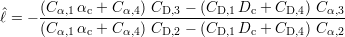 | (5.5) |
Contrairement à l’équation 5.3, cette équation n’est pas une relation linéaire et n’est pas simplifiable dans son écriture.
Les équations 5.3 et 5.4 définissent le modèle inverse qui est mis en œuvre au sein de l’algorithme de caractérisation. Elles permettent d’estimer la profondeur et la longueur d’un défaut à partir des valeurs des paramètres αc et Dc de la signature CF correspondant à ce défaut. Les coefficients de ces équations sont des constantes, définies pour un jeu de conditions de mesure.
Les modèles directs reliant les caractéristiques des défauts aux paramètres des signatures ne sont pas exacts, et l’inversion amplifie ces inexactitudes. Cela engendre des résultats d’estimation qui restent perfectibles. La connaissance de certaines spécificités de l’application étudiée permettent d’améliorer ces résultats, grâce à l’utilisation de ces informations a priori.
Les caractéristiques réelles des défauts inspectés pour cette étude permettent de déterminer de façon arbitraire quelques contraintes :
Ces deux dernières corrections n’ont pas été nécessaire pour cette étude, les estimations des dimensions n’ayant jamais dépassé ces limites.
Les conditions de laboratoire des acquisitions effectuées permettent d’appliquer l’inversion de façon aveugle sur tous les signaux CF acquis. La présence des défauts est en effet connue et la moitié des signaux CF correspond par définition à un défaut sur une zone précisément délimitée, tandis que l’autre moitié correspond à des zones sans défaut.
Cependant, dans une mise en œuvre réelle où la présence des défauts est inconnue par avance, il n’est pas logique de paramétriser des signaux CF n’ayant pas entraîné de détection. Par conséquent, seuls les signaux pour lesquels l’algorithme de détection a donné une réponse positive ont été proposés à l’algorithme de caractérisation.
De plus, l’estimation dépend fortement de la qualité du signal CF, de même que la détection. Les résultats de l’inversion ne peuvent être corrects si le signal CF a donné précédemment lieu à une non détection.
Comme cela a été vu à la sous-section 3.4, le processus d’échantillonnage spatial engendre une perte moyenne en termes de dynamique des signaux CF (cf. figure 3.15). Cette perte est statistiquement quantifiable et constante pour l’ensemble des défauts : il est donc possible de la compenser a priori, artificiellement, par une multiplication aveugle d’un coefficient constant. Le coefficient doit être défini préalablement et ne dépend que des conditions de mesure.
Cela suppose néanmoins de connaître le facteur de décimation des signaux CF à inverser ou le pas d’échantillonnage spatial des acquisitions réalisées en pratique.
La figure 5.12 montre que pour des défauts de mêmes dimensions, leur orientation engendre une différence dans la dynamique mesurée : cette dynamique est, pour un défaut d’orientation o1, systématiquement supérieure à celle d’un même défaut situé dans l’orientation o2. Le rapport de ces deux dynamiques est par ailleurs constant et indépendant des dimensions des défauts considérés : il est donc possible de compenser cette diminution par la multiplication d’un coefficient préréglé, appliquée à tous les défauts dont l’orientation aura été estimée comme étant o2. De même, l’angle d’inclinaison des signatures CF est légèrement affaibli entre les deux types d’orientations. L’ajout d’une constante permet de corriger cela.
L’effet secondaire de cette optimisation est qu’une mauvaise détection de la classe de l’orientation aura certainement des répercussions difficilement quantifiables sur l’exactitude de l’estimation des dimensions.
L’algorithme d’inversion est totalement défini par les sous-sections précédentes. Ont été abordées successivement les définitions des paramètres choisis des signaux CF et celles des caractéristiques des défauts à estimer, les méthodes d’estimation de ces caractéristiques et les possibilités d’affinage de l’algorithme. Toutes ces considérations sont synthétisées dans le schéma global de l’algorithme de caractérisation donné à la figure 5.13. L’ensemble des coefficients Ci, Cα,i, CD,i et Cp,i y figurant sont des coefficients à régler. Ils ne dépendent que des conditions de mesure.
Le réglage des coefficients doit être réalisé comme un étalonnage de l’appareil. Ces coefficients dépendent en effet uniquement des conditions de mesure, à savoir la technologie de microbobines utilisée, la stratégie d’émission-réception mise en œuvre et la fréquence des courants d’excitation. Il est donc possible de les déterminer à l’avance, à l’aide d’un jeu d’acquisitions correspondant à des défauts calibrés et de conserver ces coefficients pour l’estimation à partir de nouvelles acquisitions.
Les coefficients Ci sont déterminés par l’observation des données correspondantes. Les coefficients C1, C3 et C4 sont calculés à partir des paramètres de l’ensemble des signatures CF avant décimation. Le coefficient C2 est lui calculé par comparaison entre ces paramètres et les paramètres des signatures CF après décimation, pour une valeur de facteur de décimation ou de pas d’échantillonnage spatial donné.
Les coefficients Cα,i, CD,i et Cp,i sont calculés par la recherche des fonctions affines reliant les dimensions des défauts inspectés aux paramètres des signatures CF avant décimation, respectivement d’équations 5.1, 5.2 et 5.4.
Les équations recherchées sont des équations d’hyperplans dans les espaces formés par l’ensemble des
variables. La détermination de ces hyperplans est similaire à la détermination de la droite principale pour la
signature CF, expliquée à la sous-section 3.1.3. Pour l’obtention des coefficients de l’équation 5.4 définissant
la profondeur des défauts à partir des paramètres des signatures CF, l’estimation est réalisée par
l’estimateur des moindres carrés ordinaires, minimisant la somme des carrés des erreurs 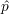 - p. Le calcul
complet nécessite une écriture sous forme matricielle de l’équation de minimisation[Wikc]. Les coefficients
sont alors obtenus par l’équation
- p. Le calcul
complet nécessite une écriture sous forme matricielle de l’équation de minimisation[Wikc]. Les coefficients
sont alors obtenus par l’équation
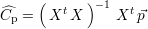
où 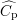 est un vecteur colonne contenant les estimations des coefficients Cp,i,
est un vecteur colonne contenant les estimations des coefficients Cp,i, 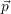 un vecteur colonne contenant
les valeurs connues des profondeurs p pour l’ensemble des défauts inspectés. X est une matrice
de trois colonnes contenant les valeurs des angles d’inclinaison dans la première colonne, les
valeurs des dynamiques principales dans la seconde colonne et des 1 dans la dernière colonne,
soit
un vecteur colonne contenant
les valeurs connues des profondeurs p pour l’ensemble des défauts inspectés. X est une matrice
de trois colonnes contenant les valeurs des angles d’inclinaison dans la première colonne, les
valeurs des dynamiques principales dans la seconde colonne et des 1 dans la dernière colonne,
soit
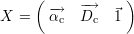
Pour l’obtention des autres coefficients, les équations 5.1 et 5.2 n’ont un sens que si Cα,1 et CD,1 sont non nuls. En les choisissant égaux à -1, il vient
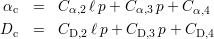
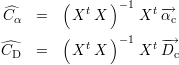
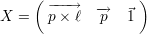
Ces coefficients sont obtenus à partir des acquisitions considérées pour l’étalonnage. Il s’agit ici des acquisitions originales, avant décimation, pour un pas d’échantillonnage spatial égal à 100 μm. Les coefficients sont réglés « une fois pour toutes ». L’algorithme ainsi réalisé peut ensuite être appliqué sur les acquisitions après décimation, qui représentent ce qui peut être obtenu de façon plus réaliste par des acquisitions de durée réduite car avec un pas d’échantillonnage spatial plus important. Pour un pas d’échantillonnage égal à la largeur d’une microbobine et dans le cas d’une sonde matricielle à deux dimensions, cette durée d’acquisition sera même tout à fait négligeable grâce à l’annulation des déplacements mécaniques.
6Dans le cas de l’orientation o1, il est relativement aisé de déterminer l’axe du défaut parmi  ou
ou  , la plus grande
dynamique étant obtenue par la sonde dont l’axe principal est parallèle au défaut. Il est donc possible d’éventuellement définir
deux « sous-cas », ce qui n’est pas réalisé ici. Dans le cas de l’orientation o2, déterminer l’axe parmi les deux possibilités est par
contre impossible.
, la plus grande
dynamique étant obtenue par la sonde dont l’axe principal est parallèle au défaut. Il est donc possible d’éventuellement définir
deux « sous-cas », ce qui n’est pas réalisé ici. Dans le cas de l’orientation o2, déterminer l’axe parmi les deux possibilités est par
contre impossible.
7Sur cette figure ainsi que sur les suivantes, les défauts d’orientation o3 sont ceux de longueur égale à 100 μm, soit les trois premiers en partant de la gauche. Les suivants correspondent effectivement à l’orientation marquée en légende, à savoir o1 pour la courbe bleue à croix et o2 pour la courbe rouge à ronds.
De même, cette figure et toutes les figures suivantes présentant l’évolution des paramètres en fonction des caractéristiques des défauts inspectés correspondent à des acquisitions effectuées dans les mêmes conditions de mesure :
8Par exemple, il est possible de prendre une moyenne pondérée entre l’estimation trouvée et 100 μm, avec un poids plus ou moins important pour la deuxième valeur selon le degré de confiance accordé à l’estimation de l’orientation.
9Dans ces travaux, il a été vu que les performances de détection restent correctes pour des facteurs de décimation inférieurs à 7 et la longueur estimée doit uniquement être positive. Au-delà, il est possible de supposer que les longueurs inférieures à 50 μm sont difficilement détectées. Le choix a été pris de faire confiance au résultat de la détection, mais il serait envisageable de faire davantage confiance au résultat de l’estimation de longueur.
10Les valeurs utilisées pour les corrections des estimations de longueur peuvent être reprises ici.
[Suivant] [Précédent] [Début] [Niveau supérieur]