5.5 Erreurs d’estimation

L’algorithme d’inversion doit être enfin évalué. Plusieurs méthodes existent pour quantifier la qualité de l’inversion. L’erreur est en général calculée pour chaque échantillon de test, et la moyenne des erreurs ainsi que leur écart-type déterminent respectivement la précision et la dispersion statistique des estimations. Les méthodes varient dans la modification des coefficients.

5.5.1 Les méthodes pour quantifier la qualité de l’inversion

Une première méthode appelée resubstitution[AB86] consiste à calculer les coefficients en prenant en compte l’ensemble des signaux acquis, et à garder ces coefficients inchangés pour évaluer les performances d’estimation sur les mêmes signaux. Cette méthode, simple à mettre en œuvre, est souvent critiquée parce qu’elle ne prend pas en considération le comportement de l’algorithme lorsqu’un cas de figure inconnu est rencontré.

Une seconde méthode, appelée Leave one out (« laissez-en un seul », LOO)[FH89], fait partie des méthodes de validation croisée. Il s’agit de calculer les coefficients grâce à l’ensemble des échantillons sauf un, et de calculer ensuite l’erreur d’inversion commise sur ce dernier. L’opération est exécutée à nouveau pour chaque échantillon. Cette méthode a la particularité d’engendrer mathématiquement un estimateur sans biais de l’erreur d’estimation. Son principal inconvénient est le temps de calcul requis, car les coefficients de l’algorithme doivent être déterminés autant de fois qu’il y a d’échantillons.

Une troisième méthode, la méthode K-fold[Koh95] (« K pliages ») est une extension de la méthode LOO, nécessitant un temps de calcul plus faible. Elle « plie » en K parties l’ensemble des échantillons, et applique la méthode LOO partie par partie. Il est ainsi nécessaire de recalculer les coefficients de l’algorithme uniquement K fois. Les résultats ont été montrés comme équivalents à ceux de la méthode LOO lorsque K > 10.

Dans le cas de cette étude, il est à la fois plus simple et plus réaliste d’appliquer une autre méthode. En effet, les méthodes décrites ci-dessus sont particulièrement utiles lorsque les acquisitions font partie simultanément des bases d’apprentissage et de test. Ce n’est pas le cas ici, car les acquisitions prises en compte dans le calcul des coefficients de l’algorithme, acquisitions constituant la base d’apprentissage, sont les signaux CF avant décimation. L’algorithme est ensuite appliqué, sans modifier ses coefficients, à l’ensemble des signaux après décimation, pour un facteur de décimation donné. Il ne s’agit donc pas d’un calcul d’erreur en resubstitution, car l’erreur d’estimation des caractéristiques est calculée sur un ensemble de signaux différents de ceux de la base d’apprentissage.

5.5.2 Erreur de classification de l’orientation

L’estimation de l’orientation consiste en une classification au sein de trois classes, explicitées à la sous-section 5.4.3. L’erreur de classification n’est donc pas continue mais booléenne, de valeur nulle ou positive. L’erreur globale peut être alors définie comme le ratio des erreurs commises sur le nombre total des échantillons de test. Le tableau 5.2 donne ces valeurs en fonction du facteur de décimation, dans les conditions de mesure utilisées à partir de la figure 5.9.

L’erreur de classification est négligeable jusqu’à n_d = 4 et reste inférieure à 5% pour un facteur de décimation inférieur à 6, soit un pas d’échantillonnage spatial égal à 600 μm. Au-delà, le pourcentage d’erreur devient grand. Pour un facteur de décimation égal à 10 correspondant à un pas d’échantillonnage spatial égal à 1 mm ou une acquisition sans déplacement mécanique pour une sonde matricielle, près d’un défaut correctement détecté sur trois est classé sur une orientation qui n’est pas la sienne. Cela pose un grave problème dans le sens où l’estimation des dimensions dépend de ce résultat.

5.5.3 Erreur d’estimation des dimensions

L’erreur est déterminée, comme expliqué à la sous-section 5.5.1, en prenant en compte l’ensemble des acquisitions. La figure 5.14 montre ces erreurs d’estimation des profondeurs et des longueurs des défauts inspectés, pour un facteur de décimation égal à 2, à 5, à 7 et à 10. Elle présente les histogrammes de ces erreurs, c’est-à-dire le nombre d’acquisitions correspondant à l’erreur portée en abscisse. Afin de rester comparables indépendamment du facteur de décimation et donc du nombre total d’acquisitions, les ordonnées de ces histogrammes sont données en pourcentage du nombre total d’acquisitions ayant engendré une détection positive.

Fig. 5.14: Histogramme en pourcentage des erreurs - p sur la profondeur estimée et - ℓ sur la longueur estimée, pour un facteur de décimation égal à 2, 5, 7 et 10

La figure 5.14 montre que la profondeur est assez bien estimée, avec une erreur 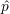-p inférieure en valeur absolue à 50 μm pour presque toutes les acquisitions à n_d = 2 et n_d = 5. Cette erreur reste encore très inférieure à 100 μm pour n_d = 7. Enfin, pour n_d = 10, la majorité des estimations donne une erreur comprise dans l’intervalle .

La longueur est moins correctement estimée. En effet, si un facteur de décimation n_d = 2 permet d’obtenir une erreur d’estimation 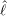- ℓ inférieure en valeur absolue à 100 μm, ce qui est encore très correct, il faut compter sur une erreur inférieure à 150 μm pour n_d = 5 et à 200 μm pour n_d = 7. L’estimation de la longueur pour n_d = 10 donne un grand nombre d’erreurs très importantes. La cause de cette difficulté d’obtenir une bonne estimation de la longueur vient principalement de la non-linéarité de l’équation 5.5 définissant 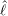. Une erreur réalisée sur l’un des deux paramètres choisis provoque une erreur d’estimation bien plus importante que pour la profondeur des défauts.

Afin de synthétiser les histogrammes de la figure 5.14, il est d’usage de calculer la moyenne et l’écart-type de l’erreur d’estimation, qui déterminent respectivement la précision et la dispersion statistique des estimations. Le tableau 5.3 contient l’ensemble de ces valeurs, en fonction du facteur de décimation.

Il apparaît dans ce tableau que l’algorithme a une tendance à surestimer en moyenne les dimensions des défauts. Cela est principalement dû à l’effet non symétrique du seuillage inférieur des dimensions, qui corrige des valeurs sous-estimées aberrantes, et introduit un biais moyen de sur-estimation. Sans ce seuillage, l’erreur d’estimation aurait un biais beaucoup plus faible voire nul, mais des valeurs négatives de dimensions estimées seraient données en résultat, ce qui est absurde.

Néanmoins, l’erreur systématique est très correcte pour l’estimation de la profondeur, quel que soit le facteur de décimation : une déviation de 30 μm peut encore être considérée comme faible comparativement à la plus petite profondeur des défauts inspectés, qui vaut seulement 100 μm. Les valeurs des écarts-types de ces estimations montrent que l’algorithme mis en œuvre fonctionne très bien pour l’estimation de la profondeur des défauts, au moins jusqu’à un facteur de décimation égal à 7, soit un pas d’échantillonnage spatial égal à 700 μm.

En ce qui concerne l’estimation de la longueur, les observations de la figure 5.14 sont confirmées : les résultats sont nettement moins bons que pour l’estimation de la profondeur des défauts. Il faut cependant souligner que la longueur est une dimension dont les valeurs considérées sont pour les défauts inspectés plus importantes que celles de la profondeur. Les valeurs des erreurs moyennes et des écarts-types sont donc logiquement plus importantes. Ces erreurs moyennes restent par ailleurs assez faibles devant la longueur moyenne des défauts. Les valeurs des écarts-types sont critiques surtout pour les défauts de faibles dimensions, et il est possible d’affirmer que les longueurs supérieures à 400 μm sont assez correctement estimées, jusqu’à un facteur de décimation égal à 7. Pour les longueurs plus faibles, l’influence de la longueur sur les signaux CF acquis est trop faible pour permettre une estimation correcte.