5.3 La paramétrisation

5.3.1 Le but de la paramétrisation

Dans le but de l’évaluation des défauts inspectés, le choix de l’inversion des signaux CF a été porté vers l’estimation des caractéristiques des défauts, c’est-à-dire le processus de caractérisation. Cependant, les signaux CF originaux contiennent un grand nombre de données, à savoir une valeur d’impédance complexe à chaque point de mesure. Cela complique fortement l’inversion, qu’elle soit itérative ou directe.

Ces données, valeurs des signaux CF situées les unes à côté des autres, sont très dépendantes entre elles, et toutes ne sont pas nécessaires pour l’inversion. Diminuer le nombre de ces données permet de simplifier le processus de caractérisation. La paramétrisation des signaux CF, par la sélection des données utiles, réalise cette simplification[Ouk97].

5.3.2 Les paramètres

Parallèlement à la nécessité de réduction du nombre de données caractérisant le signal CF, il est important que les paramètres définissent au mieux le signal, afin que le moins possible d’information contenue dans le signal ne soit perdue.

Beaucoup de paramètres peuvent être choisis. Comme expliqué à la sous-section 3.1.2, les représentations de type signatures permettent une définition plus aisée de ces paramètres et facilitent donc la paramétrisation. Il est possible de séparer les paramètres en deux classes, selon qu’ils correspondent à une signature CF ou à une combinaison de signatures CF.

5.3.2.1 Paramètres d’une signature CF

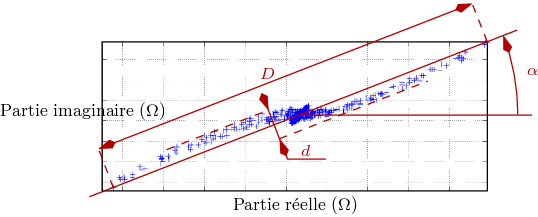
La signature CF est une des représentations possibles du signal CF. Elle a été présentée à la sous-section 3.1.2. Elle permet de visualiser l’ensemble des valeurs complexes de l’impédance acquises aux différents points de mesure, dans le plan complexe. Trois paramètres peuvent y être déterminés, indiqués sur la figure 5.4 :

• la dynamique principale D
• la dynamique secondaire d
• l’angle d’inclinaison α

Fig. 5.4: Paramétrisation d’une signature CF

La détermination de l’angle d’inclinaison est effectuée conjointement à la transformation en amplitude principale exposée à la section 3.1.3. L’angle d’inclinaison α est celui séparant l’axe réel du plan complexe de la droite de projection définie par la transformation. À partir des coefficients a et b de la droite d’équation 3.2, définis par les équations 3.6 et 3.7, l’angle d’inclinaison (en degrés) s’écrit

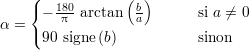
La dynamique principale est la dynamique de l’amplitude principale, calculée simplement par

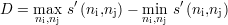
où s^′ est l’amplitude principale⁴, signal réel contenant les valeurs de la projection orthogonale du signal CF complexe s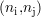 sur la droite d’angle d’inclinaison α par rapport à l’axe réel, ou encore

De même, d est la dynamique de la projection sur la droite perpendiculaire notée s^′′ et s’obtient avec

5.3.2.2 Paramètres après combinaison

La combinaison des signaux CF, décrite à la sous-section 3.2.2, permet de multiplier le nombre de ces paramètres par 3. En effet, chaque défaut, inspecté par deux sondes d’axes principaux perpendiculaires entre eux, donne trois signaux CF :

• celui du mode⁵ parallèle m_∥ comprenant les modes m_∥i et m_∥ij ;
• celui du mode perpendiculaire m_⊥ comprenant les modes m_⊥i et m_⊥ij ;
• celui du mode combiné m_c comprenant les modes m_c,i et m_c,ij.

Ainsi sont obtenus les paramètres α_∥, α_⊥, α_c, D_∥, D_⊥, D_c, d_∥, d_⊥, d_c. Le mode combiné produit un signal CF identique pour deux défauts perpendiculaires entre eux : il sera souvent préférable d’utiliser, parmi les paramètres définis précédemment, ceux calculés sur des signatures CF combinées.

D’autres paramètres peuvent être calculés à partir des trois signaux CF correspondant à un même défaut, en utilisant plusieurs paramètres parmi les précédents. En faire une liste exhaustive serait fastidieux et relativement peu utile, à cause des multiples possibilités. Un grand nombre de ces possibilités a néanmoins été étudié. Cette étude a permis de sélectionner les paramètres les plus intéressants, comme présenté à la sous-section 5.4.2.