|
|
[Précédent] [Fin] [Niveau supérieur]
Les deux sections précédentes ont permis l’établissement d’un algorithme de détection applicable sur chaque signal CF acquis (section 4.1) et d’une méthode statistique permettant à la fois de déterminer quelles conditions de mesure offrent les meilleures performances de détection, et quel réglage de l’algorithme il faut choisir pour obtenir ces meilleures performances (section 4.2). Cet algorithme et la méthode des courbes COR ont été utilisés sur l’ensemble des acquisitions effectuées. Ils permettent ainsi de connaître les performances de détection qui peuvent être statistiquement attendues des sondes réalisées pour la gamme des défauts considérés dans cette étude.
La figure 4.8 présente les courbes COR obtenues pour les différentes fréquences des CF, dans le cas d’acquisitions faites avec les deux technologies de microbobines, pour la stratégie ERE-. La sonde à microbobines CI a des performances nettement moins bonnes que celle à bobines micromoulées : pour la stratégie ERE-, la seconde sonde obtient une courbe COR « parfaite », c’est-à-dire passant par le point optimal (0,1), pour presque toutes les fréquences, contrairement à la première.
|
|
Ces courbes utilisent les 30 défauts de la pièce-échantillon, soit les orientations oi et oj, sans combinaison. La PFA est évaluée à l’aide de 30 zones suffisamment éloignées des défauts, pour chaque évaluation. L’obtention des courbes parfaites signifie qu’il existe pour ces conditions de mesure au moins un seuil permettant grâce à l’algorithme défini à la section 4.1 de détecter tous les défauts sans déclencher une seule FA. Cette détection est parfaite dans le cas de l’utilisation de la sonde à bobines micromoulées. La sonde à microbobines CI, avec le meilleur réglage, permet à 3 MHz de détecter tous les défauts (PDC = 1) mais avec 6,7% de FA. La figure 4.8 confirme donc la conclusion de l’étude du RSB à la section 3.6 : la technologie des bobines micromoulées permet d’obtenir des meilleurs résultats de détection que la technologie des microbobines CI.
Cinq stratégies d’émission-réception ont été conçues dans le cadre de ces travaux, dans le but de voir leurs performances de détection comparées et de déterminer ainsi la meilleure d’entre elles. Afin de pouvoir les évaluer et déterminer la meilleure stratégie d’émission-réception, il est important de comparer leurs performances de détection. La figure 4.9 présente les courbes COR optimales7 au sens de la maximisation du critère ASC, pour chacune des cinq stratégies d’émission-réception et pour chacune des deux technologies de microbobines. Il y apparaît que les stratégies RER, ERE- et ER sont capables avec la sonde à bobines micromoulées d’atteindre le point optimal (0,1). Pour la sonde à microbobines CI, la meilleure courbe reste celle correspondant à la stratégie ERE- à une fréquence de 3 MHz.
Pour plus de détail, la figure 4.10 trace l’ASC pour l’ensemble des fréquences d’acquisition. Un classement des performances des différentes stratégies d’émission-réception peut être établi ainsi :
En simplifiant, ce classement peut s’écrire
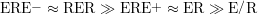
|
|
De plus, les courbes de la figure 4.10 confirment à nouveau et de façon très globale, pour l’ensemble des stratégies d’émission-réception et l’ensemble des fréquences des CF, la capacité de la sonde à bobines micromoulées à obtenir des meilleures performances de détection. Les figures dans la suite de ce chapitre ne considéreront donc plus que les mesures effectuées à l’aide de la sonde à bobines micromoulées, dans le cas de la stratégie d’émission-réception ERE-.
Le pas d’échantillonnage spatial des acquisitions influence directement le nombre de points de mesure appartenant à la zone de signal utile et par suite l’efficacité de l’algorithme de détection. La variation du pas d’échantillonnage est ici obtenue, comme expliqué à la section 3.4, par décimation. Plus le facteur de décimation est fort, plus grand est le pas d’échantillonnage et plus petit est le nombre de points de mesure conservés dans l’image décimée. Un facteur de décimation égal à 10 correspond, pour la sonde à bobines micromoulées, à un pas d’échantillonnage spatial égal à la largeur des microbobines. Une reconstruction est ensuite possible à partir de l’image décimée, par un suréchantillonnage exposé à la section 3.5. Les meilleurs résultats ont été observés pour un facteur de suréchantillonnage ne égal au facteur de décimation nd.
La figure 4.11 compare, dans le cas de la stratégie ERE- mise en œuvre avec la sonde à bobines micromoulées, les performances de détection de la sonde en fonction de la décimation opérée, toujours suivie d’un suréchantillonnage de même facteur. Elle trace l’évolution du critère ASC (figure 4.11-a) en fonction de la fréquence, pour un facteur de décimation compris entre 1 et 10, ainsi que les courbes COR correspondantes, pour une fréquence des CF de 5 MHz (figure 4.11-b).
La dégradation des courbes COR nécessairement entraînée par le processus de décimation est quasi-nulle jusqu’à nd = 6 : la détection est presque parfaite encore pour cette valeur, ce qui est une conclusion un peu plus optimiste que celle du calcul du RSB. À nd = 7 soit un pas d’échantillonnage spatial égal à 700 μm, l’ASC diminue légèrement. Les courbes s’éloignent plus nettement du point optimal (0,1) pour un facteur de décimation plus grand.
|
|
La figure 4.12 détaille cette évolution par les valeurs, pour chaque courbe COR, des PDC et PFA correspondant aux performances optimales8 de la sonde. Pour nd = 7, plus de 98% des défauts sont détectés, et à peine 1% de fausses alarmes sont déclenchées : ce résultat est tout à fait acceptable. Pour nd = 8, ces taux sont encore corrects avec respectivement 93% de DC et 2% de FA. Enfin, pour nd = 10, le taux d’ED dépasse les 15%, ce qui peut être considéré comme des performances moyennes. Ce cas est néanmoins intéressant car il correspond à un pas d’échantillonnage spatial égal à 1 mm, c’est-à-dire la longueur du côté des microbobines : avec une matrice de microbobines, l’acquisition peut être réalisée sans déplacement mécanique.
Les figures 4.8 à 4.12 montrent des courbes COR et les ASC correspondantes, calculées à partir des acquisitions faites pour les défauts suivant les orientations oi et oj, sans combinaison. Or, l’orientation d’un défaut comparativement à l’orientation principale de la sonde modifie le signal CF mesuré, comme l’a montré la section 3.2, et par conséquent sa probabilité de détection. L’influence de l’orientation du défaut sur les performances de détection de la sonde doit donc être quantifiée.
La figure 4.13 montre, pour la sonde à bobines micromoulées avec la stratégie ERE- et pour un facteur de décimation nd = 7, les valeur de l’ASC pour les courbes COR dans trois possibilités :
Cette figure présente aussi les valeurs des PDC qui correspondent au réglage optimal du paramètre de
l’algorithme. Contrairement à la figure 4.12, le réglage du seuil de détection est déterminé par d’autres
courbes COR, prenant en compte l’ensemble des défauts. En effet, pour une fréquence des CF donnée, les
inspections des défauts suivant les orientations oi, oj et 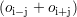 engendrent trois courbes COR
particulières. Mais l’ensemble des défauts, dans un environnement réaliste où les défauts sont mélangés,
correspond à une quatrième courbe COR. Cette courbe sert à déterminer le réglage optimal de l’algorithme
de détection, qui est ainsi optimal pour l’ensemble des cas possibles. La probabilité de détecter un défaut
suivant une orientation est alors obtenue au sein de la courbe COR particulière, au point correspondant au
seuil ainsi déterminé.
engendrent trois courbes COR
particulières. Mais l’ensemble des défauts, dans un environnement réaliste où les défauts sont mélangés,
correspond à une quatrième courbe COR. Cette courbe sert à déterminer le réglage optimal de l’algorithme
de détection, qui est ainsi optimal pour l’ensemble des cas possibles. La probabilité de détecter un défaut
suivant une orientation est alors obtenue au sein de la courbe COR particulière, au point correspondant au
seuil ainsi déterminé.
Les défauts situés suivant l’orientation oi sont bien mieux détectés que les
autres9.
Malgré une valeur d’ASC relativement proche, une nette différence, de près de 10%, peut être visualisée
entre les taux de détection de ces défauts et ceux des défauts d’orientations 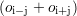 . En effet,
les dynamiques des signaux CF pour les premiers défauts sont généralement plus élevées que
pour les seconds : prendre le seuil de détection global conduit à un compromis qui a tendance à
diminuer le seuil de détection pour les défauts suivant oi tout en augmentant celui des défauts
suivant
. En effet,
les dynamiques des signaux CF pour les premiers défauts sont généralement plus élevées que
pour les seconds : prendre le seuil de détection global conduit à un compromis qui a tendance à
diminuer le seuil de détection pour les défauts suivant oi tout en augmentant celui des défauts
suivant 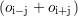 . Les taux de DC et par suite les probabilités de détection varient dans le sens
opposé.
. Les taux de DC et par suite les probabilités de détection varient dans le sens
opposé.
Intérêt des modes de combinaison d’orientations
Une combinaison des images a été mise en place à la sous-section 3.2.2 (cf. figure 3.12). Il
s’agit de l’addition complexe, en chaque point de mesure, des valeurs d’impédances acquises
par deux jeux de microbobines dont les orientations principales sont perpendiculaires entre
elles10.
Cela doit permettre de détecter avec les mêmes performances un défaut qui serait dans l’orientation oi ou
dans l’orientation oj. Il est intéressant de savoir ce qu’il advient pour l’ensemble des défauts, y compris ceux
suivant les orientations oi-j et oi+j.
La figure 4.14 montre la valeur du critère ASC en fonction de la fréquence pour un facteur de décimation variable compris entre 1 et 10. Ces valeurs sont tracées à la figure 4.14-a pour des courbes COR prenant en compte simultanément les quatre orientations de défauts inspectés, sans combinaison. La valeur de l’ASC quantifie donc la qualité globale de détection du dispositif, indépendamment de l’orientation des défauts. Sur la figure 4.14-b, les courbes COR prennent en compte uniquement les deux modes combinés mc,i et mc,ij. La valeur de l’ASC quantifie alors, comme précédemment, la qualité de détection indépendamment de l’orientation des défauts, mais cette fois après combinaison des signaux acquis.
|
|
Le fait de réaliser la détection par l’intermédiaire des modes combinés plutôt que par les acquisitions avant combinaison permet d’augmenter sensiblement la valeur de l’ASC. Cela permet, selon la forme des courbes COR correspondantes, de gagner en moyenne, pour un facteur de décimation nd = 7, environ la moitié du taux d’erreurs de détection, soit de 6% à 3% d’ED, tandis que la PFA reste à peu près constante et très faible.
Afin de résumer les divers résultats et conclusions de cette section, deux tableaux sont établis ci-après. Le premier réunit les données de comparaison entre les deux technologies de microbobines et les cinq stratégies d’émission-réception. Le second tableau énonce les meilleurs résultats de détection en fonction du facteur de décimation choisi.
Le tableau 4.2 contient toutes les valeurs optimales du critère ASC. Il détaille chaque technologie de microbobines, chaque stratégie d’émission-réception et trois valeurs du facteur de décimation ; il ne prend en compte que, d’une part les défauts situés selon les orientations oi et oj, d’autre part la combinaison de ces deux orientations au sein du mode mc,i. Les valeurs optimales des PDC et des PFA sur les courbes COR correspondantes sont aussi incluses dans ce tableau. Il permet ainsi de dégager trois conclusions importantes au sujet des performances de détection :
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le tableau 4.3 montre les meilleurs résultats obtenus avec la sonde à bobines micromoulées et la stratégie d’émission-réception ERE-, en considérant tous les défauts, c’est à dire les orientations oi, oj, oi-j et oi+j, uniquement par combinaison : il s’agit donc des performances par l’utilisation des modes mc,i et mc,ij.
Il convient de rappeler que nd est le facteur de la décimation qui est appliquée sur les signaux CF avant de quantifier ses performances, et que la décimation est suivie d’un suréchantillonnage de même facteur avant l’évaluation par l’algorithme de détection. Cela correspond à un pas d’échantillonnage spatial des acquisitions égal à nd × 100 μm. Le temps d’acquisition « normalisé » est calculé pour chaque facteur de décimation, en fonction du temps de l’acquisition effectuée avec un pas d’échantillonnage spatial égal à 100 μm. Ce pourcentage est le temps que mettrait la même sonde à trois microbobines pour évaluer une même zone. Le gain de temps est donc très grand, même pour un facteur de décimation égal à 5. Dans le cas d’une matrice à deux dimensions de microbobines, le cas nd = 10 est celui pour lequel la sonde n’est plus déplacée pour effectuer l’ensemble des acquisitions : le temps d’acquisition est alors très faible, voire nul.
|
L’augmentation de l’erreur commise est expérimentalement une fonction logarithmique12 de nd : une valeur de 7 ou 8 permet de contenir les taux d’erreurs dans des limites tout-à-fait acceptable. Au-delà, la détection ne peut plus être considérée comme totalement fiable. Néanmoins, cette étude permet de quantifier la perte de performances de détection correspondant à un temps d’acquisition nul, soit 8,5% d’ED et 9,9% de FA.
7Chaque courbe correspond à une seule fréquence, optimale pour la stratégie d’émission-réception et la technologie de microbobines considérées.
8Chaque point sur la figure 4.12 correspond donc à une courbe COR entière, soit un grand nombre de signaux et un réglage que l’on peut considérer comme définitif pour les conditions considérées. On parle de « Probabilité de détection correcte optimale » et de « Probabilité de fausse alarme optimale », au sens où ce sont les performances optimales qui peuvent être atteintes dans ces conditions de mesure.
9Les défauts suivant l’orientation oj, bien que situés selon une orientation a priori très mauvaise, sont plus efficacement
détectés que les orientations oi-j et oi+j, car leur signal CF possède une aussi grande dynamique et recouvre une plus grande
surface grâce à l’apparition des lobes secondaires suivant l’axe 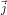 . Cette étendue acquiert un rôle important pour la détection
lorsque le pas d’échantillonnage devient grand.
. Cette étendue acquiert un rôle important pour la détection
lorsque le pas d’échantillonnage devient grand.
10Ici, ces mesures combinées sont calculées à partir de mesures réalisées avec une même sonde sur deux défauts identiques perpendiculaires entre eux, après rotation d’une des deux images.
11Il convient de comparer les performances globales des deux types de microbobines pour un facteur de décimation nd = 5, où ces performances ne sont pas encore trop dégradées.
12La corrélation linéaire entre le logarithme de ces pourcentages et la valeur de nd est très forte, avec le carré du coefficient de corrélation R2 supérieur à 0,98.
[Précédent] [Début] [Niveau supérieur]