4.1 L’algorithme de détection

La section 3.6 met en place une technique très utilisée de quantification de la qualité d’un signal, le calcul du rapport signal sur bruit. Cette technique ne suffit pas pour mettre en œuvre un processus de détection des défauts, car une valeur du RSB de l’ordre du critère de Rose ne permet pas d’estimer correctement si le signal CF correspond ou non à un défaut. De plus, une valeur du RSB est propre à un signal donné, et chaque jeu de conditions de mesure, de même que chaque défaut ou chaque positionnement relatif de la sonde par rapport au défaut, peut donner un RSB différent.

Par conséquent, la détection doit être réalisée indépendamment des traitements déjà effectués, d’une mesure de dynamique ou d’un calcul de RSB. Il est préférable pour ce faire d’utiliser un algorithme de détection dédié.

4.1.1 Qu’est-ce qu’une détection ?

La détection d’un défaut est un processus de décision binaire. Il s’agit de donner une estimation positive ou négative de la présence d’un défaut. Cette réponse est donnée grâce à un critère de décision défini en général au sein d’un algorithme. L’état de détection, résultat binaire du processus de détection, s’écrit de façon générale

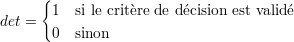
L’état de détection dépend d’un ou de plusieurs paramètres, comme ce sera le cas pour les algorithmes décrits ci-après. Ces paramètres doivent être alors réglés en fonction des conditions de mesure, éventuellement des propriétés de la cible comme la rugosité, voire des défauts recherchés.

Deux cas réels concernant la présence d’un défaut sont possibles, représentés usuellement par deux hypothèses H₀ et H₁

• H₀ : le signal CF ne correspond à aucun défaut ;
• H₁ : le signal correspond à un défaut.

En fonction de la valeur de l’état de détection det, quatre combinaisons sont possibles. Elles sont présentées dans le tableau 4.1. Les deux erreurs possibles sont l’erreur de détection (ED) et la fausse alarme (FA). Une ED correspond à une pièce défectueuse non diagnostiquée comme telle, qui peut devenir potentiellement dangereuse selon le défaut qu’elle contient. Cette erreur survient particulièrement lorsque le défaut présent est de très faibles dimensions, ou si les conditions de mesure sont particulièrement défavorables pendant l’acquisition. Une FA est la détection erronée d’un défaut inexistant. Elle contribue à la réparation ou la perte d’une pièce pourtant intacte, et constitue par conséquent un coût injustifié pour le processus de fabrication ou de révision de l’appareil.

4.1.2 Un premier algorithme : le seuillage simple

L’algorithme le plus évident est certainement le seuillage simple. Il donne une réponse positive de détection si, pour au moins un seul point de mesure 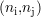, la valeur s 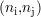du module du signal CF est supérieure au seuil de détection θ fixé, soit

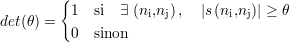
θ est un réglage du critère de décision. Il peut être fixé pour chaque jeu de conditions de mesure, restant alors identique pour l’ensemble des évaluations effectuées dans les mêmes conditions.

Il est éventuellement possible d’ajuster le seuil de détection en fonction des défauts recherchés. En effet, l’amplitude des signaux CF dépend de la taille des défauts et il est possible de se donner une taille minimale de défaut à visualiser, en considérant que les défauts de taille moins importante ne sont pas nocifs pour l’application visée. Il en découle une valeur de seuil, qui dépend des conditions de mesure mais aussi des dimensions minimales des défauts recherchés.

Cet algorithme est extrêmement simple à mettre en œuvre. Cependant, sa simplicité a pour conséquence un taux de FA potentiellement assez élevé. En effet, le moindre point de mesure correspondant à une valeur de signal bruitée supérieure au seuil θ déclenche une détection, ce qui entraîne nécessairement un grand nombre d’états det = 1 sous l’hypothèse H₀. Augmenter le seuil θ peut alors permettre de diminuer le nombre de fausses alarmes, mais engendre une perte certaine de détections correctes (DC) sur les défauts de faibles dimensions.

4.1.3 Un deuxième algorithme : le seuillage moyenné

Une façon d’améliorer l’algorithme à seuillage simple est de réaliser un seuillage prenant en compte les points de mesure adjacents au point considéré. L’algorithme choisi est représenté à la figure 4.2. Il est important de noter que le signal CF à mettre en entrée de l’algorithme doit être réel positif. Il peut s’agir soit du module du signal CF, soit de la valeur absolue de l’amplitude principale définie à la section 3.1.3. L’algorithme est constitué de 3 étapes, deux seuillages entre lesquels est effectuée une convolution.

4.1.3.1 Premier seuillage simple

Un premier seuillage simple est effectué, avec un seuil de détection θ, comme celui réalisé au sein du premier algorithme. L’image résultante s₁ est une image binaire, dans laquelle chaque valeur est remplacée par un 1 ou un 0 si elle est supérieure ou inférieure à θ, soit

Le seuil θ est le seuil de détection, paramètre de l’algorithme. Il doit être réglé lors d’une étape préliminaire en fonction de l’ensemble des signaux CF acquis, afin de ne plus être modifié ultérieurement. Contrairement au seuillage du premier algorithme, celui-ci n’est pas suivi immédiatement de la prise de décision du processus de détection.

4.1.3.2 Convolution avec un masque

Le résultat de ce premier seuillage est une image binaire. Si le seuil est suffisamment faible, un grand nombre de points de mesure correspondront à un résultat non nul. Les points de mesure situés dans de la zone de signal utile, de valeur s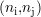 déterministe et supérieure au seuil, seront tous « allumés » tandis que seule une partie d’entre eux le sera hors de cette zone, de façon dispersée. Il est alors possible de déterminer une zone comme étant une zone de signal utile si elle est remplie uniformément de valeurs binaires s₁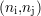 non nulles : il suffit par conséquent de rechercher dans l’image seuillée un nombre suffisant de points de mesure non nuls adjacents.

Pour ce faire, l’image binaire s₁ est convoluée à une autre image binaire m. Cette image est un masque contenant une « tâche » connexe, c’est-à-dire constituée de points adjacents où la valeur est non nulle ; les points ne faisant pas partie de cette tâche correspondent à des valeurs nulles. Elle peut être de forme quelconque : un carré plein est une forme très simple, facile et rapide à générer ; un disque demande un calcul un peu plus complexe¹ mais est plus réaliste par rapport aux images CF présentées au chapitre 3. Le masque est « normé » : la somme de l’ensemble des valeurs vaut 1. Les deux valeurs possibles de m ne sont pas 0 et 1 mais 0 et 1∕n_m, où n_m est le nombre de points à valeur non nulle.

La notion de convolution correspond, comme cela a été expliqué dans la sous-section 3.1.1.3, à une notion de filtrage. Ici, le filtre utilisé possède une réponse impulsionnelle équivalente en deux dimensions à une porte en une dimension : il s’agit donc d’un filtre moyenneur. Ainsi, un moyennage² des valeurs de s₁ est effectué sur une zone aussi large que la tâche de m. La convolution s’écrit

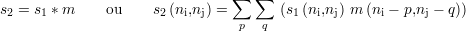(4.1)

Les valeurs du signal résultant s₂ sont ainsi nécessairement comprises entre 0 et 1 et subissent en chaque point l’influence d’un ensemble de valeurs correspondant à l’étendue entière de la tâche.

La taille de cette tâche peut par ailleurs devenir un paramètre éventuel de l’algorithme, car elle a une influence non négligeable sur son résultat, comme le seuil de détection θ. En effet, diminuer cette taille jusqu’à transformer la tâche en un point unique rend cet algorithme équivalent au premier algorithme présenté à la sous-section précédente. À l’inverse, si la taille de la tâche est trop grande, l’algorithme risque de ne jamais donner de résultat positif.

Dans cette étude, la sous-section 3.1.1 a montré que les images CF possèdent toutes des lobes d’étendue spatiale similaire. L’influence de la taille de la tâche de m a été observée dans le cas des signaux CF acquis pour ces travaux, ce qui a permis de la fixer empiriquement à une valeur de performances optimales, offrant les meilleurs résultats indépendamment de tout autre paramètre d’influence. Pour un masque contenant un disque, le diamètre utilisé ici vaut 1800 μm et 700 μm respectivement pour les signaux CF produits par les sondes à microbobines CI et à bobines micromoulées³.

4.1.3.3 Recherche de valeur maximale

Si s₂ comporte une seule valeur s₂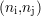 égale à 1, cela signifie qu’au sein de l’image s₁, beaucoup de points de mesure 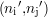situés autour du point 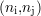ont leur valeur initiale s 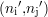supérieure au seuil de détection θ. Il s’agit bien de ce qui est attendu comme étant l’image d’un défaut⁴. Il suffit donc de rechercher cette valeur maximale égale à 1 pour savoir si l’algorithme doit donner une réponse positive ou non. Un deuxième seuillage, cette fois effectué sur s₂ et de seuil 1, permet cela. Après l’application du critère de décision sur ce seuillage, il vient

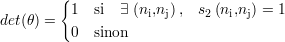
Ainsi, l’état de détection est égal à 1 si et seulement si au moins un point de mesure de l’image CF s est entouré d’un nombre n_m suffisant de points où la valeur de s est supérieure à θ, n_m étant défini par le masque. Cela a pour effet d’éliminer les zones de bruit où il est statistiquement difficile de trouver autant de points agglomérés dépassant le seuil de détection. Comparativement au premier algorithme, il est alors possible de diminuer fortement ce seuil sans pour autant déclencher de fausse alarme.

¹La génération d’un disque de rayon r au sein d’une matrice nécessairement carrée et par exemple de côté 2 r demande en effet de créer une matrice contenant à chaque point la valeur de la distance relativement au centre positionné au point (r,r). Ensuite, un seuillage inversé doit être réalisé avec un seuil égal à r afin de donner une valeur non nulle aux points de distance au centre inférieure à r. Ceci est beaucoup plus complexe que générer un carré plein, qui est simplement une matrice carrée remplie de 1.

²Il est aussi possible de considérer l’opération réalisée par l’équation 4.1 comme une corrélation croisée des deux images. En effet, une corrélation croisée entre s₁ et m s’écrit

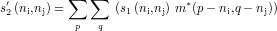
La conjugaison complexe signifiée par l’opérateur ^* est ici inactive car m est réelle, de même que la symétrie spatiale par rapport à la diagonale car m possède cette symétrie. Les deux calculs sont donc bien équivalents. Or le calcul d’une corrélation croisée quantifie, comme son nom l’indique, une ressemblance entre les deux signaux considérés. Le calcul de s₂^′ traduit ainsi la recherche des points où l’image binaire s ₁ ressemble en partie à la tâche présente sur le masque m. La ressemblance parfaite intervient au point où la corrélation croisée est maximale et ici égale à 1.

³Ces valeurs vérifient les résultats de l’analyse fréquentielle réalisée à la sous-section 3.4.2.

⁴Les images présentées au chapitre 3 montrent systématiquement deux tâches. Ne rechercher qu’une seule tâche n’est pas moins précis, et permet de gagner en rapidité d’exécution par une taille de masque moins importante.